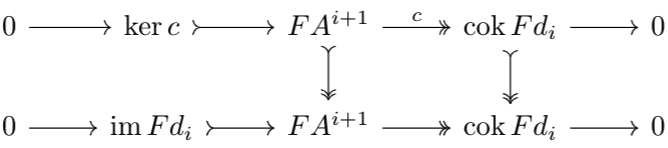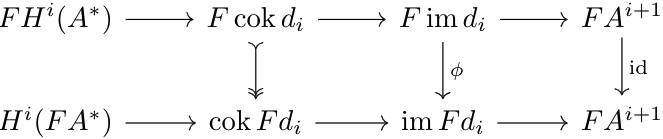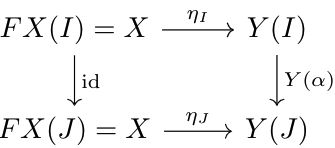Interaction of Universal Properties
This post in some sense is an extension of Universal Properties since we'll understand how the constructions defined in that post interact with each other.
Exact Functors
If \(F:\mathfrak A\to\mathfrak B\) is an additive functor between abelian categories, \(F\) is right-exact iff \(A\to B\to C\to 0\) being exact implies \(F(A)\to F(B)\to F(C)\to0\) is exact. \(F\) is left-exact iff \(0\to A\to B\to C\) being exact implies \(0\to F(A)\to F(B)\to F(C)\) is exact. \(F\) is exact if it is left and right exact.
If \(F\) is a contravariant additive functor, we say \(F\) is right-exact iff \(A\to B\to C\to 0\) being exact implies \(F(C)\to F(B)\to F(A)\to0\) is exact. \(F\) is left-exact iff \(0\to A\to B\to C\) being exact implies \(0\to F(C)\to F(B)\to F(A)\) is exact.
Some basic facts about exact functors
- Exact functors send exact sequences to exact sequences.
- Given \(S\), a multiplicative subset of commutative ring \(A\), the localization functor \(Mod_A\to Mod_{S^{-1}A}\) is exact.
- \((-)\otimes_A M\) for any \(M\in Mod_A\) is right-exact.
- \(\Hom(M,-),\Hom(-,M)\) are both left-exact. More generally, for any abelian category \(\rmC\), \(C\in\rmC\), the following are both left-exact:$$\Hom(C,-),\Hom(-,C):\mathfrak C\to Mod_\mathbb Z$$
Characterizations of Exact Functors
Let \(f:A\to B\) be a kernel of \(g:B\to C\). Thus, \(0\to A\xrightarrow fB\xrightarrow gC\) is exact, so \(0\to F(A)\to F(B)\to F(C)\) is exact. Thus, \(F(A)\to F(B)\) is a monomorphism, so \(\im F(A)\to F(B)\) is just \(F(A)\to F(B)\). And \(\ker F(B)\to F(C)\) is \(F(A)\to F(B)\) since left-exact functors preserve kernels. To see that this is an alternate characterization of left-exactness, note that if additive \(F\) sends kernels to kernels, then for any exact sequence \(0\to A\xrightarrow fB\xrightarrow gC\), \(f\) is a kernel of \(g\). So, \(F(f)=\ker F(g)\), but this implies \(0\to F(A)\to F(B)\to F(C)\) is exact.
A similar proof works for contravariant functors, and the dual proof shows the rest.In Lemma 5 of Abelian Categories where the existence of all finite limits and colimits was proved, the kernel and product structures were used to generate the limit, and by duality, the coproduct and cokernel structures to generate the colimit. Left exact functors preserve kernels and direct sums, and right exact functors preserve cokernels and direct sums, so this shows that they preserve limits/colimits respectively.
We've seen already that products and kernels can be written as limits, and coproducts and cokernels as colimits, so a functor that preserves all finite limits is left-exact, and a functor that preserves all finite colimits is right-exact. Thus, this is an alternate characterization.
Interactions of Universal Properties
Given a cochain complex $$A^*:\qquad0\to A^0\xrightarrow{d_0}A^1\ldots$$we can use \(F\) to morph to a new cochain complex $$FA^*:0\to FA^0\xrightarrow{Fd_0}FA^1\ldots$$To see why the result is a cochain complex, observe that $$Fd_{i+1}\circ Fd_i=F(d_{i+1}\circ d_i)=F0=0$$Via the post (Co)homology and Exactness, we know that we can factor both \(FA^*\) into short exact sequences as follows:$$0\to\im Fd_i\to FA^{i+1}\to\cok Fd_i\to0\tag1$$$$0\to H^i(FA^*)\to\cok Fd_{i-1}\to\im Fd_i\to0\tag2$$Similarly, we can factor \(A^*\), and then by right-exactness of \(F\), end up with the following exact sequences$$FH^i(A^*)\to F\:\cok d_{i-1}\to F\:\im d_i\to0\tag3$$$$F\:\im d_i\to FA^{i+1}\to F\:\cok d_i\to0\tag4$$Note that since right-exact functors preserve cokernels, \(F\:\cok d_i\cong \cok Fd_i\). Thus, consider the following commutative diagram:
The two vertical maps are isomorphisms, so thus by the discussion in Co(chain) Morphisms, there exists an isomorphism between \(\ker c\) and \(\im Fd_i\). In particular, \(\im Fd_i\) is the kernel of \(FA^{i+1}\to F\:\cok d_i\) in sequence \((4)\).
Since sequence \((4)\) is exact, the map \(F\:\im d_i\to FA^{i+1}\to F\:\cok d_i\) is the \(0\) map by the cocycle condition, and thus by kernel properties, there exists a unique map \(\phi:F\:\im d_i\to \im Fd_i\) such that \(F\:\im d_i\to FA^{i+1}\) in sequence \((4)\) factors into \(\phi\) and the kernel morphism \(\im Fd_i\to FA^{i+1}\). To encode this information, we can consider the following diagram:
By construction of \(\phi\), the square consisting of the \(\im\) and \(FA^{i+1}\) terms commutes. And, since the first and third vertical maps are isomorphisms, the rectangle consisting of the \(\cok\)and \(FA^{i+1}\) terms commutes. Thus, the square consisting of the \(\im\)and \(\cok\)terms commutes. Thus, the map $$FH^i(A^*)\to F\:\cok d_i\to\cok Fd_i\to\im Fd_i$$is the map $$FH^i(A^*)\to F\:\cok d_i\to F\:\im d_i\xrightarrow\phi\im Fd_i$$which is \(0\) by the cocycle condition. Thus, by the kernel property of \(H^i(FA^*)\), there exists a unique morphism \(FH^i(A^*)\to H^i(FA^*)\) that commutes with the diagram.
A dual argument will show that for a left-exact functor, we get a unique morphism \(H^i(FA^*)\to FH^i(A^*)\). And since uniqueness is preserved by composition, for exact functors, these unique morphisms are inverses of each other, and thus are isomorphisms.We need to show that \(GA\to GA_i\) satisfies the limit conditions. Let \(W\to GA_i\) be a collection of maps commuting as in the limit definition. Thus, by the adjointness of \(F,G\), \(FW\to A_i\) is a collection of maps commuting as in the limit definition. Thus, there exists a unique map \(FW\to A\) such that the maps \(FW\to A_i\) are factored as \(FW\to A\to A_i\). Thus, the maps \(W\to GA_i\) are factored as \(W\to GA\to GA_i\). The rest of the limit conditions for \(GA\) hold by functors respecting composition. Thus, \(GA\) satisfies the conditions for the limit.
If we let \(Func(\rmA,\rmB)\) be the category of functors from \(\rmA\to\rmB\), and morphisms be natural transformations, consider the case in which \(\rmA\) is a small category and \(\rmB\) contains all limits/colimits of functors in \(Func(\rmA,\rmB)\). For any element \(B\) in \(\rmB\), there is a functor in \(Func(\rmA,\rmB)\) which sends all objects to \(B\) and all morphisms to \(\id_B\). We call this functor \(\Delta B\), the constant functor on \(B\). Thus, there is a functor \(F:\rmB\to Func(\rmA,\rmB)\) which sends objects to their constant functors, and morphisms to the corresponding natural transformation.
If we let \(G\) be the functor (unique up to isomorphism) \(Func(\rmA,\rmB)\to\rmB\) which sends functors to their limits, observe that we can define a map \(\phi:\Mor(FX, Y)\to\Mor(X, GY)\) with \(X\in\rmB\), \(Y\in Func(\rmA,\rmB)\) as follows. Let \(\eta\in\Mor(\Delta X,Y)\) (\(FX=\Delta X\)), with \(\eta_A:\Delta X(A)\to Y(A)\) for each \(A\in\rmA\). By the definition of natural transformation, the following diagram commutes for any \(\alpha:I\to J\in\rmA\):
By the limit properties of \(\varprojlim Y\) with projection maps \(y_I:\varprojlim Y\to Y(I)\) for all \(I\in\rmA\), there exists a unique map \(\psi\in\Mor(X,\varprojlim Y)\) such that for all \(I\in\rmA\), \(\eta_I=y_I\circ\psi\). Since \(\varprojlim Y=GY\), we can define \(\phi(\eta)=\psi\). It's not too hard to show that this definition is a natural bijection, which shows that \(G\) is a right adjoint to the constant functor. Dually, the colimit functor is a left adjoint to the constant functor.
Now, we want to show that a particular type of colimit (filtered colimits: colimits with indexing category filtered) commutes with kernels, and thus is exact when viewed as a functor.
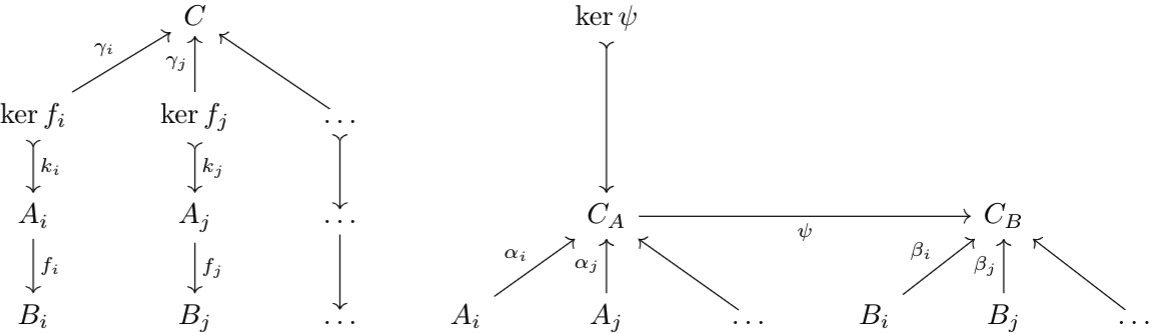
Let's establish some notation. We call \(\varinjlim\ker f_i\) \(C\), \(\varinjlim F\) \(C_A\), and \(\varinjlim G\) \(C_B\). The embedding maps for \(C\) are denoted \(\gamma_i:\ker f_i\to C\). Thus, we have the following diagram:
Note that for any map \(\tau:A_i\to A_j\), the induced map \(\tau^*:\ker f_i\to\ker f_j\) satisfies \(k_j\circ\tau^*=\tau\circ k_i\). So, letting \(g_i:\ker f_i\to C_A\) be the map \(\alpha_i\circ k_i\), for any induced map \(tau^*:\ker f_i\to\ker f_j\), $$g_j\circ\tau^*=\alpha_j\circ k_j\circ\tau^*=\alpha_j\circ\tau\circ k_i=\alpha_i\circ k_i=g_i$$where the penultimate equality comes from the colimit properties of \(C_A\). Thus, by the colimit property of \(C\), there exists a map \(\zeta:C\to C_A\) such that for all \(i\in I\), $$\zeta\circ\gamma_i=g_i=\alpha_i\circ k_i$$Observe that for all \(i\), $$\psi\circ\zeta\circ\gamma_i=\psi\circ\alpha_i\circ k_i=\beta_i\circ f_i\circ k_i=0$$Thus, there exists a unique map \(\eta:C\to C_B\) by colimit properties of \(C\) such that for all \(i\)$$\eta\circ\gamma_i=\psi\circ\zeta\circ\gamma_i=0$$Thus, \(\eta=0\), and by uniqueness, \(\psi\circ\zeta=0\).
By kernel properties of \(\ker\psi\), there exists a unique morphism \(\phi:C\to\ker\psi\) such that \(\ker\psi\circ\phi=\zeta\). Thus, we've constructed our natural epimorphism \(\phi\). It is epimorphic since colimits commute with colimits, and cokernels are a type of colimit.
To see that \(\phi\) is an isomorphism when \(I\) is a filtered partially ordered set and \(\rmA=Mod_R\), notice that the characterization provided for the colimit of a filtered partially ordered set for subcategories of Set also holds for \(Mod_R\) (this is relatively straightforward to show). Moreover, we get injectivity of \(\phi\) as follows: if there exists some non-zero \(y\in C\) such that \(\phi(y)=0\), then there exists some \(x\neq0\in\ker f_i\) for some \(i\in I\) such that \(\gamma_i(x)=y\). Thus, $$\ker\psi\circ\phi\circ\gamma_i=\alpha_i\circ k_i$$But, the left side evaluates \(x\to0\), but the right side is monic, and thus does not. This is a contradiction, which proves injectivity. Since injectivity is the same thing as monic for \(Mod_R\), we are done. Note that this proof essentially works for any category that is "similar enough" to Set to use the alternate characterization of the colimit.