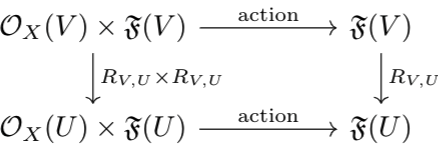\ie \cf

$\newcommand{\norm}[1]{\\|#1\\|} \newcommand{\etal} \newcommand{\ie} \newcommand{\eg} \newcommand{\cf} \newcommand{\rank}{\text{rank}} \newcommand{\tr}{\text{tr}} \newcommand{\mor}{\text{Mor}} \newcommand{\hom}{\text{Hom}} \newcommand{\id}{\text{id}} \newcommand{\obj}{\text{obj}} \newcommand{\pr}{\text{pr}} \newcommand{\ker}{\text{ker}} \newcommand{\coker}{\text{coker}} \newcommand{\im}{\text{im}} \newcommand{\vol}{\text{vol}} \newcommand{\bbA}{\mathbb A} \newcommand{\bbB}{\mathbb B} \newcommand{\bbC}{\mathbb C} \newcommand{\bbD}{\mathbb D} \newcommand{\bbE}{\mathbb E} \newcommand{\bbF}{\mathbb F} \newcommand{\bbG}{\mathbb G} \newcommand{\bbH}{\mathbb H} \newcommand{\bbI}{\mathbb I} \newcommand{\bbJ}{\mathbb J} \newcommand{\bbK}{\mathbb K} \newcommand{\bbL}{\mathbb L} \newcommand{\bbM}{\mathbb M} \newcommand{\bbN}{\mathbb N} \newcommand{\bbO}{\mathbb O} \newcommand{\bbP}{\mathbb P} \newcommand{\bbQ}{\mathbb Q} \newcommand{\bbR}{\mathbb R} \newcommand{\bbS}{\mathbb S} \newcommand{\bbT}{\mathbb T} \newcommand{\bbU}{\mathbb U} \newcommand{\bbV}{\mathbb V} \newcommand{\bbW}{\mathbb W} \newcommand{\bbX}{\mathbb X} \newcommand{\bbY}{\mathbb Y} \newcommand{\bbZ}{\mathbb Z} \newcommand{\cA}{\mathcal A} \newcommand{\cB}{\mathcal B} \newcommand{\cC}{\mathcal C} \newcommand{\cD}{\mathcal D} \newcommand{\cE}{\mathcal E} \newcommand{\cF}{\mathcal F} \newcommand{\cG}{\mathcal G} \newcommand{\cH}{\mathcal H} \newcommand{\cI}{\mathcal I} \newcommand{\cJ}{\mathcal J} \newcommand{\cK}{\mathcal K} \newcommand{\cL}{\mathcal L} \newcommand{\cM}{\mathcal M} \newcommand{\cN}{\mathcal N} \newcommand{\cO}{\mathcal O} \newcommand{\cP}{\mathcal P} \newcommand{\cQ}{\mathcal Q} \newcommand{\cR}{\mathcal R} \newcommand{\cS}{\mathcal S} \newcommand{\cT}{\mathcal T} \newcommand{\cU}{\mathcal U} \newcommand{\cV}{\mathcal V} \newcommand{\cW}{\mathcal W} \newcommand{\cX}{\mathcal X} \newcommand{\cY}{\mathcal Y} \newcommand{\cZ}{\mathcal Z} \newcommand{\rmA}{\mathfrak A} \newcommand{\rmB}{\mathfrak B} \newcommand{\rmC}{\mathfrak C} \newcommand{\rmD}{\mathfrak D} \newcommand{\rmE}{\mathfrak E} \newcommand{\rmF}{\mathfrak F} \newcommand{\rmG}{\mathfrak G} \newcommand{\rmH}{\mathfrak H} \newcommand{\rmI}{\mathfrak I} \newcommand{\rmJ}{\mathfrak J} \newcommand{\rmK}{\mathfrak K} \newcommand{\rmL}{\mathfrak L} \newcommand{\rmM}{\mathfrak M} \newcommand{\rmN}{\mathfrak N} \newcommand{\rmO}{\mathfrak O} \newcommand{\rmP}{\mathfrak P} \newcommand{\rmQ}{\mathfrak Q} \newcommand{\rmR}{\mathfrak R} \newcommand{\rmS}{\mathfrak S} \newcommand{\rmT}{\mathfrak T} \newcommand{\rmU}{\mathfrak U} \newcommand{\rmV}{\mathfrak V} \newcommand{\rmW}{\mathfrak W} \newcommand{\rmX}{\mathfrak X} \newcommand{\rmY}{\mathfrak Y} \newcommand{\rmZ}{\mathfrak Z} \newcommand{\paren}[1]{( #1 )} \newcommand{\Paren}[1]{\left( #1 \right)} \newcommand{\bigparen}[1]{\bigl( #1 \bigr)} \newcommand{\Bigparen}[1]{\Bigl( #1 \Bigr)} \newcommand{\biggparen}[1]{\biggl( #1 \biggr)} \newcommand{\Biggparen}[1]{\Biggl( #1 \Biggr)} \newcommand{\abs}[1]{\lvert #1 \rvert} \newcommand{\Abs}[1]{\left\lvert #1 \right\rvert} \newcommand{\bigabs}[1]{\bigl\lvert #1 \bigr\rvert} \newcommand{\Bigabs}[1]{\Bigl\lvert #1 \Bigr\rvert} \newcommand{\biggabs}[1]{\biggl\lvert #1 \biggr\rvert} \newcommand{\Biggabs}[1]{\Biggl\lvert #1 \Biggr\rvert} \newcommand{\card}[1]{\left| #1 \right|} \newcommand{\Card}[1]{\left\lvert #1 \right\rvert} \newcommand{\bigcard}[1]{\bigl\lvert #1 \bigr\rvert} \newcommand{\Bigcard}[1]{\Bigl\lvert #1 \Bigr\rvert} \newcommand{\biggcard}[1]{\biggl\lvert #1 \biggr\rvert} \newcommand{\Biggcard}[1]{\Biggl\lvert #1 \Biggr\rvert} \newcommand{\norm}[1]{\lVert #1 \rVert} \newcommand{\Norm}[1]{\left\lVert #1 \right\rVert} \newcommand{\bignorm}[1]{\bigl\lVert #1 \bigr\rVert} \newcommand{\Bignorm}[1]{\Bigl\lVert #1 \Bigr\rVert} \newcommand{\biggnorm}[1]{\biggl\lVert #1 \biggr\rVert} \newcommand{\Biggnorm}[1]{\Biggl\lVert #1 \Biggr\rVert} \newcommand{\iprod}[1]{\langle #1 \rangle} \newcommand{\Iprod}[1]{\left\langle #1 \right\rangle} \newcommand{\bigiprod}[1]{\bigl\langle #1 \bigr\rangle} \newcommand{\Bigiprod}[1]{\Bigl\langle #1 \Bigr\rangle} \newcommand{\biggiprod}[1]{\biggl\langle #1 \biggr\rangle} \newcommand{\Biggiprod}[1]{\Biggl\langle #1 \Biggr\rangle} \newcommand{\set}[1]{\lbrace #1 \rbrace} \newcommand{\Set}[1]{\left\lbrace #1 \right\rbrace} \newcommand{\bigset}[1]{\bigl\lbrace #1 \bigr\rbrace} \newcommand{\Bigset}[1]{\Bigl\lbrace #1 \Bigr\rbrace} \newcommand{\biggset}[1]{\biggl\lbrace #1 \biggr\rbrace} \newcommand{\Biggset}[1]{\Biggl\lbrace #1 \Biggr\rbrace} \newcommand{\bracket}[1]{\lbrack #1 \rbrack} \newcommand{\Bracket}[1]{\left\lbrack #1 \right\rbrack} \newcommand{\bigbracket}[1]{\bigl\lbrack #1 \bigr\rbrack} \newcommand{\Bigbracket}[1]{\Bigl\lbrack #1 \Bigr\rbrack} \newcommand{\biggbracket}[1]{\biggl\lbrack #1 \biggr\rbrack} \newcommand{\Biggbracket}[1]{\Biggl\lbrack #1 \Biggr\rbrack} \newcommand{\ucorner}[1]{\ulcorner #1 \urcorner} \newcommand{\Ucorner}[1]{\left\ulcorner #1 \right\urcorner} \newcommand{\bigucorner}[1]{\bigl\ulcorner #1 \bigr\urcorner} \newcommand{\Bigucorner}[1]{\Bigl\ulcorner #1 \Bigr\urcorner} \newcommand{\biggucorner}[1]{\biggl\ulcorner #1 \biggr\urcorner} \newcommand{\Biggucorner}[1]{\Biggl\ulcorner #1 \Biggr\urcorner} \newcommand{\ceil}[1]{\lceil #1 \rceil} \newcommand{\Ceil}[1]{\left\lceil #1 \right\rceil} \newcommand{\bigceil}[1]{\bigl\lceil #1 \bigr\rceil} \newcommand{\Bigceil}[1]{\Bigl\lceil #1 \Bigr\rceil} \newcommand{\biggceil}[1]{\biggl\lceil #1 \biggr\rceil} \newcommand{\Biggceil}[1]{\Biggl\lceil #1 \Biggr\rceil} \newcommand{\floor}[1]{\lfloor #1 \rfloor} \newcommand{\Floor}[1]{\left\lfloor #1 \right\rfloor} \newcommand{\bigfloor}[1]{\bigl\lfloor #1 \bigr\rfloor} \newcommand{\Bigfloor}[1]{\Bigl\lfloor #1 \Bigr\rfloor} \newcommand{\biggfloor}[1]{\biggl\lfloor #1 \biggr\rfloor} \newcommand{\Biggfloor}[1]{\Biggl\lfloor #1 \Biggr\rfloor} \newcommand{\lcorner}[1]{\llcorner #1 \lrcorner} \newcommand{\Lcorner}[1]{\left\llcorner #1 \right\lrcorner} \newcommand{\biglcorner}[1]{\bigl\llcorner #1 \bigr\lrcorner} \newcommand{\Biglcorner}[1]{\Bigl\llcorner #1 \Bigr\lrcorner} \newcommand{\bigglcorner}[1]{\biggl\llcorner #1 \biggr\lrcorner} \newcommand{\Bigglcorner}[1]{\Biggl\llcorner #1 \Biggr\lrcorner} \newcommand{\Rnn}{\R_{\ge 0}} \DeclareMathOperator{\Tr}{Tr} \DeclareMathOperator{\Inf}{Inf} \DeclareMathOperator{\min}{min} \DeclareMathOperator{\max}{max} \DeclareMathOperator{\argmax}{arg\,max} \DeclareMathOperator{\argmin}{arg\,min} \DeclareMathOperator{\E}{\mathbb E} \DeclareMathOperator{\pE}{\tilde{\mathbb E}} \DeclareMathOperator{\Pr}{\mathbb P} \DeclareMathOperator{\Det}{\textbf{Det}} \DeclareMathOperator{\Perm}{\textbf{Perm}} \DeclareMathOperator{\Sym}{\textbf{Sym}} \DeclareMathOperator{\Pow}{\textbf{Pow}} \DeclareMathOperator{\Gal}{\textbf{Gal}} \DeclareMathOperator{\Aut}{\textbf{Aut}} \notag$

$\newcommand{\sleq}{\ensuremath{\preceq}} \notag$

$\newcommand{\transpose}[1]{\ensuremath{#1{}^{\mkern-2mu\intercal}}} \newcommand{\dyad}[1]{\ensuremath{#1#1{}^{\mkern-2mu\intercal}}} \newcommand{\nchoose}[1]{\ensuremath} \newcommand{\generated}[1]{\ensuremath{\langle #1 \rangle}} \notag$

\newcommand{\eqdef}{\mathbin{\stackrel{\rm def}{=}}}  \newcommand{\R} % real numbers  \newcommand{\N}} % natural numbers  \newcommand{\Z} % integers  \newcommand{\F} % a field  \newcommand{\Q} % the rationals  \newcommand{\C}{\mathbb{C}} % the complexes  \newcommand{\poly}}  \newcommand{\polylog}}  \newcommand{\loglog}}}  \newcommand{\zo}{\{0,1\}}  \newcommand{\suchthat}  \newcommand{\pr}[1]{\Pr\left[#1\right]}  \newcommand{\deffont}{\em}  \newcommand{\getsr}{\mathbin{\stackrel{\mbox{\tiny R}}{\gets}}}  \newcommand{\Exp}{\mathop{\mathrm E}\displaylimits} % expectation  \newcommand{\Var}{\mathop{\mathrm Var}\displaylimits} % variance  \newcommand{\xor}{\oplus}  \newcommand{\GF}{\mathrm{GF}}  \newcommand{\eps}{\varepsilon}  \notag

$\newcommand{\eps}{\varepsilon} \notag$

\no

$\newcommand{\textprob}[1]{\text{#1}} \newcommand{\mathprob}[1]{\textbf{#1}} \newcommand{\Satisfiability}{\textprob{Satisfiability}} \newcommand{\Mor}{\textprob{Mor}} \newcommand{\Hom}{\textprob{Hom}} \newcommand{\cok}{\textprob{cok}} \newcommand{\ker}{\textprob{ker}} \newcommand{\im}{\textprob{im}} \newcommand{\coim}{\textprob{coim}} \newcommand{\id}{\textprob{id}}$

Next |

| Previous

Presheaves and Sheaves

100%

Presheaves
Sheaves
Pushforwards
Ringed Spaces

Now that we've motivated the idea of sheaves and built some preliminary tools, let's define sheaves. Our data will be contained within elements of Set, but equivalently, we could use any set + additional structure, like $Mod_R$, Ring, etc. In fact, one could even use objects in categories that aren't easily interpretable as sets, although that requires a bit more effort. We'll discuss this approach briefly but won't use it at all.

Presheaves

Given a topological space $(X,\tau)$ ($\tau$ is a basis for the topology, not necessarily the topology itself), a presheaf $\rmF$, represented as $\rmF\rightharpoondown X$ (NOTE: this is not standard notation), is the following data:

To each $U\in\tau$, we have a set $\rmF(U)$ (sometimes denoted as $\Gamma(U,\rmF)$ or $H^0(U,\rmF)$). The elements of $\rmF$ are called sections of $\rmF$ over $U$. If $U$ isn't specified, $U=X$. In this case, we call the sections global sections. In our motivating example, the sections were the differentiable morphisms $U\to\mathbb R$.
For each $V\subset U$, there exists a restriction map $R_{U,V}:\rmF(U)\to\rmF(V)$.
For all $U\in\tau$, $R_{U,U}=\id_{\rmF(U)}$.
For all $W\subset V\subset U$, $R_{U,W}=R_{V,W}\circ R_{U,V}$.

This definition should be intuitively clear based on our motivation from the post Understanding Sheaves. There are quite a few interesting ways to interpret the definition of presheaves.

Given topological space $(X,\tau)$, we can partially order $\tau$ by inclusion and thus form a poset category. From now on in this blog, $\tau$ will both represent the topology and the category of open sets of $X$ viewed as a poset category. The data of a contravariant function $G:\tau\to\textbf{Set}$ is the same as that of a presheaf.

This is just a basic check of the definition. $G(U)$ for any $U$ gives us a set, $G(V\to U)$ gives us a morphism $G(U)\to G(V)$, which we call $R_{U,V}$, $$R_{U,U}=G(U\to U)=G(\id)=\id$$and condition $4$ of the presheaf is equivalent to functors respecting composition. Thus, the data is identical.

Obviously, if our data was stored as objects in set-like category $\rmC$, the contravariant functor would be $\tau\to\rmC$ instead of $\tau\to\textbf{Set}$.

We define the stalk in two ways, similar to how we did it in Understanding Sheaves. For the constructive approach, we define it as the set of germs $(f,U)$ with $p\in U\in\tau$, $f\in\rmF(U)$, under the equivalence relation $(f,U)\sim(g,V)$ iff there exists $W\in\tau\subset U,V$ such that $f\vert_W=g\vert_W$.

For the categorical approach, let $B_p$ be the subcategory of $\tau$ consisting only of those open sets around $p$. Let $H_p$ be the restriction of the functor $\rmF$ to $B_p$. Then, the stalk is just $\rmF_p=\varinjlim H_p$.

We call the image of any $f\in\rmF(U)$ in $\rmF_p$ for an open set $U$ with $p\in U$ the germ of $f$ at $p$. We sometimes notate the germ of $f$ at $p$ as $f_p$, although this can be confusing at times since $f_p$ is an overloaded term.

Sheaves

A sheaf, represented as $\rmF\rightharpoonup X$ (NOTE: this is not standard notation), is a presheaf $\rmF\rightharpoondown X$ that satisfies the following conditions for any $\{U_i\}$ open cover of $U$:

If $f_1,f_2\in\rmF(U)$ such that for all $i$, $f_1\vert_{U_i}=f_2\vert_{U_i}$, then $f_1=f_2$.
If there exists $f_i\in\rmF(U_i)$ for each $i$ such that for any $i,j$, $f_i\vert_{U_i\cap U_j}=f_j\vert_{U_i\cap U_j}$, then there exists $f\in\rmF(U)$ such that $f\vert_{U_i}=f_i$ for all $i$.

Condition $5$ is often called the identity axiom, and Condition $6$ is often called the gluability axiom. Again, these conditions shouldn't be intuitively difficult given the motivation in Understanding Sheaves.

The sheaf axioms automatically imply that $\rmF(\varnothing)$ is a final object of the category, as the gluability axiom implies that there is a map from $\rmF(U)\to\rmF(\varnothing)$ for every $U\in\tau$ and the identity axiom implies any two such maps must be equal. However, this isn't necessarily implied in presheaves. We'll see an example of this in the constant presheaf.

Some examples and non-examples:

If we take a presheaf on $\bbR$ with the topological basis of bounded open sets, and the sheaf maps open sets to bounded functions, then any continuous unbounded function (like $\id$) will be defined on each of the bounded open sets, so the gluability axiom is violated. But, all of the presheaf conditions are trivially satisfied.
A general condition encompassing the sheaf definition is as follows: for any open cover $\{U_i\}$ of $U$, $\varprojlim\rmF$ exists and is equal to $\rmF(U)$. Gluability comes from the existence of the limit (since limit projections are epic, the glued map is just the preimage), and identity comes from the following argument.
Suppose that the projection maps $\rmF(U)\to\rmF(U_i)$ all send $f$ and $g$ to the same map. Then, the map $\rmF(U)\to\rmF(U)$ that sends to $f\to g$, $g\to f$ and everything else to itself will commute with projection. Thus, by limit properties, it is the unique map that commutes with projection. But, the identity map also commutes with projection, so $f=g$.
Real valued continuous functions on a topological space $X$ form a natural sheaf.
Differentiable, continuous, smooth, or ordinary functions form a sheaf on a smooth manifold $X$.
We can restrict a sheaf $\rmF\rightharpoonup X$ to an open subset $U\subset X$ by restricting to only those open sets that are subsets of $U$. This object, denoted by $\rmF\vert_U$, is also a sheaf.
Consider the pointed topological space $p\in X$ and some set $S$. We can generate a sheaf by sending all open sets containing $p$ to $S$, and the rest to $E$, where $E$ is any singleton (more generally, if we wanted to define sheaves over other categories, we would want $E$ to be a final object of the category). Thus, the restriction maps would be $\id_S$, and the unique maps $S\to E$ and $S\to E$. We call the resulting structure the skyscraper sheaf. Observe that $p$ isn't necessarily the only point with a non-trivial stalk (to see why, think about some non-$T_1$ topologies).
We might consider modifying the skyscraper sheaf to send all open sets to $S$ and all restrictions to the identity. Unfortunately, this doesn't always generate a sheaf. We call the resulting object the constant presheaf.
To see why this structure isn't always a sheaf, note that if $S$ isn't a singleton, it violates the sheaf condition by the remark above. Even if we patched the constant presheaf's definition to send $\varnothing$ to a final object (which is how we will define the constant presheaf from now on), we still are in hot water. Consider the discrete space $\{a,b\}$ with $S=\bbZ$. Letting $f_{\{a\}}=1$, $f_{\{b\}}=2$, it's easy to see that the conditions for the gluability axiom are met, but clearly there is no element of $\bbZ$ that is both $1,2$ simultaneously. When a constant presheaf is a sheaf, we don't call it a constant sheaf: we'll define that next. (As a thought experiment before I spoil the answer in a future post: what conditions would be required to ensure that this construction is a sheaf? What failed us here was disconnectedness. Is that the only issue?)
To ensure that the previous notion creates a sheaf, we modify the construction as follows: $\rmF(U)$ now is the set of functions $U\to S$ which are continuous if $S$ is endowed with the discrete topology (we call this condition locally constant since it is equivalent to the condition requiring for any $p\in U$ and section $f$ of $U$, there exists an open neighborhood around $p$ on $f$ is constant). The restriction maps are the obvious ones. We check that this forms a sheaf by showing gluability (everything else is obvious): for any open cover $U=\bigcup\{U_i\}$, and $f_i:U_i\to S$ for each $i$, let $f(x)=f_i(x)$ if $x\in U_i$. I claim that $f:U\to S$ is locally constant. For any $s\in S$, $f^{-1}(s)=\bigcup f_i^{-1}(s)$, which implies that $f^{-1}(s)$ is open since each $f_i^{-1}(s)$ is open in $U_i$, and thus $U$. This shows gluability. We call this sheaf the constant sheaf. We sometimes notate it as $\underline S$.
As a generalization of the previous bullet, given topological spaces $X,Y$, the sheaf that sends $U$ to the set of continuous functions $U\to Y$ is a sheaf.
To generalize even further, given a continuous map $\mu:Y\to X$, let $\rmF(U)$ be the set of continuous functions $s:U\to Y$ such that $\mu\circ s=\id\vert_U$. This is a sheaf on $X$, and is also why the elements of $\rmF(U)$ are called sections (since they are "sections" of $\mu$).
Given a topological group $Y$, the sheaf $F\rightharpoonup Y$ given by sending $U$ to the group of continuous functions $U\to Y$ gives a sheaf of groups (the data is in Grp, rather than Set).

Memorizing these examples isn't particularly helpful, but they should give you some intuition as to what sorts of objects can be viewed as sheafs.

There is an alternate way of characterizing sheaves via the étalé espace of a presheaf. Let's understand what that means.

Let $\rmF\rightharpoondown X$. Let $F=\bigsqcup\limits_{p\in X}\rmF_p$. Thus, we have a natural map $\pi:F\to X$ which sends elements of $\rmF_p$ to $p$. For each section $f\in \rmF(U)$, we have the subset $\{(x,f_x)\mid x\in U\}$ of $F$. We topologize $F$ by letting its topology be the coarsest one which makes all of these subsets open. Moreover, $$\bigcup\limits_{f\in\rmF(U)}\{(x,f_x)\mid x\in U\}=\pi^{-1}(U)$$

This implies that $\pi$ is continuous. We call $F$ the space of sections of $\rmF$ (or in French, étalé espace).

Properties of the space of sections (won't be proven since we don't need them, but are interesting to think about regardless):

The sets $\{(x,f_x)\mid x\in U\}$ form a topological basis for the topology on $F$.
There exists a natural interpretation of pullbacks in $F$.
The map sending $\rmF\to F$ is an equivalence of categories (This statement is not well-defined right now since we haven't talked about how sheaves form categories. However, once we establish a notion of sheaf morphisms, think about how spaces of sections respect sheaf morphisms).
Sheafification (to be defined in a future post) has a natural interpretation in $F$.

From a historical perspective, sheaves were initially studied through spaces of sections. However, they have rather complicated structure, and the topology on them is often unmotivated. This is why this approach is not as favored today.

Pushforwards

Let $\pi:X\to Y$ be continuous and $\rmF\rightharpoondown X$. For any open set $V\subset Y$, let $$\pi_*\rmF(V)=\rmF(\pi^{-1}(V))$$$\pi_*\rmF$ is a presheaf, and a sheaf if $\rmF$ is.

Observe that for any open sets $U\subset V\subset Y$, $\pi^{-1}(U)\subset\pi^{-1}(V)\subset X$ are open sets too, so let $R_{\pi_*\rmF(V),\pi_*\rmF(U)}=R_{\pi^{-1}(V),\pi^{-1}(U)}$. This obviously satisfies the presheaf requirements. If $\rmF$ is a sheaf, $\rmF(U)$ is the limit of the open cover $\{U_i\}$ for any open cover $U_i$ of $U$. Thus, for any open cover $V_i$ of $V\subset Y$, $\pi^{-1}(V_i)$ is an open cover of $\pi^{-1}(V)\subset X$, so $\pi_*\rmF(V)$ is the limit of the open cover $V_i$, which implies that $\pi_*\rmF$ is a sheaf by example 2.

We call the sheaf $\pi_*\rmF$ the pushforward of $\rmF$ by $\pi$.

The skyscraper sheaf is the pushforward of the constant sheaf $\underline S$ on a singleton space $\{p\}$, under the inclusion morphism $i_p:\{p\}\to X$. Thus, we often notate the skyscraper sheaf as $i_{p,*}\underline S$ (Awful notation, I know. You can blame Vakil for that).

There is a natural morphism of stalks $\phi:(\pi_*\rmF)_q\to\rmF_p$ assuming that $\pi(p)=q$. To see how, observe that for any open set $V$ containing $q$, $\pi^{-1}(V)$ contains $p$, so there exists a natural embedding $\pi_*\rmF(V)=\pi^{-1}(V)\to\rmF_p$ by the colimit definition of $\rmF_p$. By the colimit properties of $(\pi_*\rmF)_q$, there exists a unique $\phi$ which is natural in the obvious sense. This suggests that $\pi\mapsto\pi_*$ should be a contravariant functor in some natural sense. We may talk about this in a later post (I might be overcommitting my time here, but who knows)

Ringed Spaces

A very important example (so important, in fact, that it deserves its own section) of sheaves is that of ringed spaces. Let $\cO_X$ be a sheaf of rings on $X$. We then call $(X,\cO_X)$ a ringed space. $\cO_X$ is called the structure sheaf of the ringed space. Sections of $\cO_X$ are called functions on $U$ (Vakil notes that in some texts, these functions are called regular functions).

The restriction $\cO_X\vert_U$ for an open set $U\subset X$ is denoted $\cO_U$. The stalk at point $p$ is notated $\cO_{X,p}$. We now define the notion of $\cO_X$ modules. A sheaf of Ab (i.e., a sheaf that takes sections as elements of abelian groups) $\rmF$ is called a $\cO_X$-module iff for each open $U\subset X$, $\rmF(U)$ is a module of $\cO_X(U)$, such it respects restriction (i.e., the diagram below commutes for all open $U\subset V\subset X$)

Since Ab is the same thing as $Mod_\bbZ$, $Mod_R$ can be seen as a generalization of Ab. In the same way, $\cO_X$ modules generalize the sheaf of abelian groups, as the latter is the same as a $\underline\bbZ$-module. So, proving things about $\cO_X$ modules also proves things about sheaves of abelian groups.

Given a ringed space $(X,\cO_X)$ and $\cO_X$ module $\rmF$, $\rmF_p$ can naturally be interpreted as a $\cO_{X,p}$ module for all $p\in X$.

$\cO_{X,p}=\varinjlim\cO_X(U)$ and $\rmF_p=\varinjlim\rmF(U)$ with the limits over those open sets containing $p$. Each $\rmF(U)$ has a well-defined module structure over $\cO_X(U)$. So, we define the action $\cO_{X,p}\times\rmF_p\to\rmF_p$ as follows. Given $(r,x)\in\cO_{X,p}\times\rmF_p$, let $U$ be an open set such that $\cO_X(U)$ has an element $s$ which embeds into $r$ via the colimit maps, and likewise, let $V$ be an open set such that $\rmF(V)$ has an element $y$ which embeds into $x$ via the colimit maps. Since the open sets are filtered, there exists $W\subset U,V$, and thus, let $z\in\rmF(W)$ be the result of the action on the elements $R_{U,W}(s)$ and $R_{V,W}(y)$. Let $z^*$ be the image of $z$ in $\rmF_p$. Thus, $(r,x)\mapsto z^*$ is a map of the desired form, which is well-defined as a module action since action commutes with restriction, and due to the module properties of the colimiting objects.

Top