Preliminaries
These preliminaries aren't in the text I'm referring to, but I've been somewhat frustrated with the lack of rigor in how the text treats functions and their properties, so I believe that this setup is important. If you think this is pedantic, feel free to skip this post.
Normed Vector Spaces
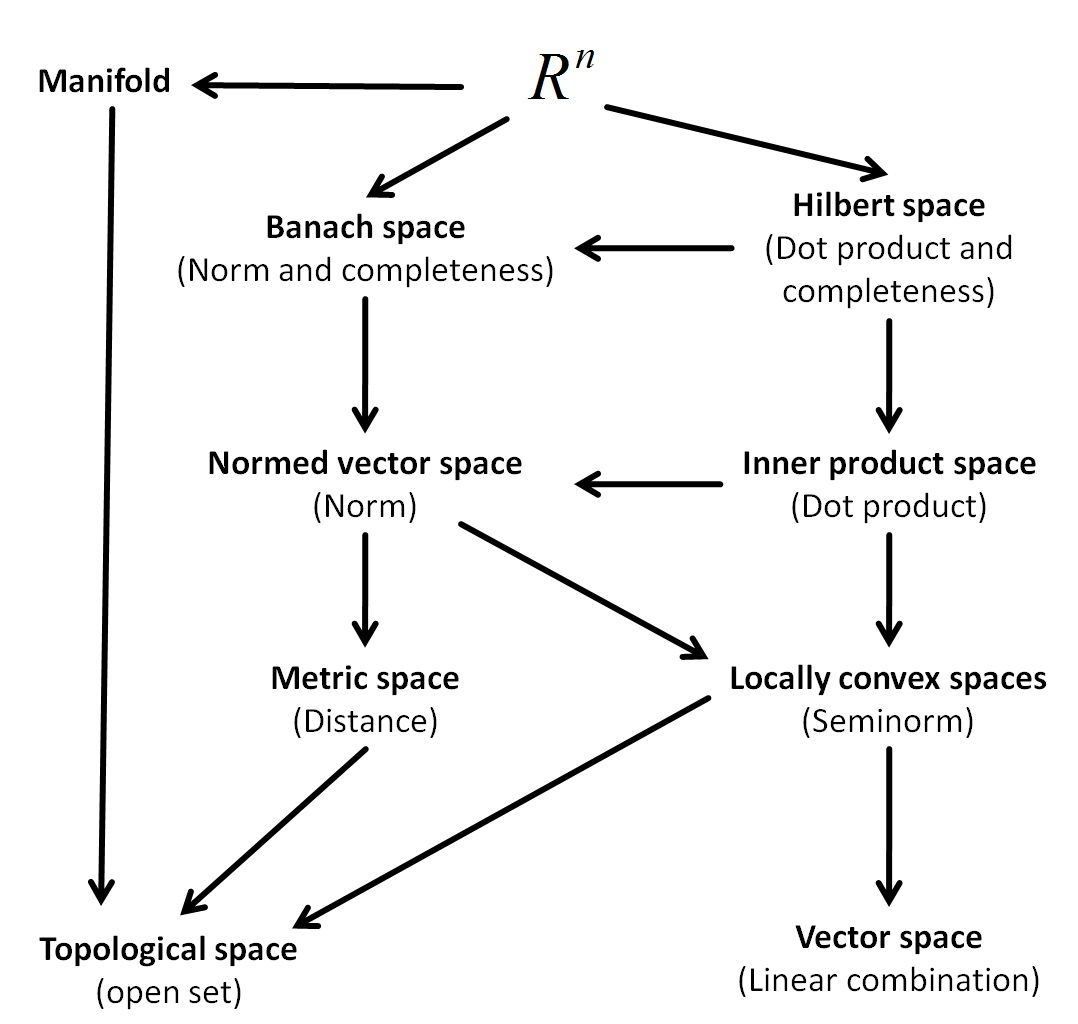
Our goal is to find a general space that contains all of our functions of interest, while still being narrow enough to have interesting and useful properties. In mathematics, we have a large hierarchy of space structures, many of which are generalizations of others. In the diagram below, we have a layout of some common structures that \(\bbR^n\) belong to, with the arrow relationship indicating increasing generality.
This diagram is by no means complete. For example, we could add Riemannian manifolds in between \(\bbR^n\) and manifolds. Or perhaps Hausdorff spaces between manifolds and topological spaces. However, this diagram will be more than sufficient for our purposes. I'm assuming that the reader already has exposure to modules, vector spaces, measure spaces, and metric space.
Let's begin by defining normed vector spaces.
- For any \(c\in\bbR\) and \(x\in X\), \(\Norm{cx}=\card c\Norm x\)
- The function \(d(x,y)=\Norm{y-x}\) makes \(X\) into a metric space.
If we want to avoid using metric spaces in our definition, we can use the following four requirements to characterize normed vector spaces.
- Non-negativity: \(\Norm x\geq0\) for all \(x\in X\)
- Homogeneity: \(\card c\Norm x=\Norm{cx}\) for all \(c\in\bbR\), \(x\in X\)
- Triangle Inequality: \(\Norm{x+y}\leq\Norm x+\Norm y\) for all \(x,y\in X\)
- Distinguishability: \(\Norm x>0\) for all \(x\neq0\in X\).
Unfortunately, there are many potential normed vector spaces that satisfy all of the requirements besides distinguishability. These occur so frequently that we give them a name: semi-normed spaces. Fortunately for us, there's a very convenient way of converting partially semi-normed spaces into normed vector spaces. I'll do this within the context of function spaces but it isn't too hard to see how this may generalize.
Call the largest vector space on which \(S\) is defined \(\rmF^*\). Let \(\rmF^*_0=S^{-1}(0)\cap\rmF^*\). I claim that \(\rmF^*_0\) is a vector space.
- Given \(x,y\in\rmF^*_0\), \(x+y\in\rmF^*\), and \(0\leq S(x+y)\leq S(x)+S(y)=0\), so \(x+y\in S^{-1}(0)\). Thus, \(x+y\in\rmF^*_0\).
- Given \(c\in\bbR\), \(cx\in\rmF^*\), and \(S(cx)=\card cS(x)=0\), so \(cx\in \rmF^*_0\)
Let \(\rmF=\rmF^*/\rmF^*_0\), the quotient vector space. I claim that \(S\) is well defined on the equivalence classes of \(\rmF\). Given \(x,y\in\rmF^*\) such that \(y-x\in\rmF^*_0\) (and thus \(x-y\in\rmF^*_0\)), we have $$S(x)\leq S(y)+S(x-y)=S(y)$$$$S(y)\leq S(x)+S(y-x)=S(x)$$Thus, \(S\) is a seminorm on \(\rmF\). Moreover, if \(S([f])=0\) (where \([f]\) is the equivalence class of \(f\)), then \([f]=[0]\), so \(S\) is distinguishable and thus a norm.
Perhaps the most relevant example of the theorem above is \(L_p\) spaces.
Before we begin the proof, observe that not all measurable functions are part of the domain of \(\Norm{}_p\). Some are sent to \(\infty\), which is ill-defined. We call those functions that the partial seminorm sends to a finite value p-integrable. Let \(\rmF^*\) be the collection of \(p\) integrable functions.
First, we show that \(\Norm{}_p\) is a seminorm on \(\rmF^*\).
- Non-negativity: An integral of a non-negative function can never be negative by monotonicity of integration. A supremum is also non-negative.
- Homogeneity: $$\left(\int|cf(x)|^pd\mu\right)^{1/p}=|c|\left(\int|f(x)|^pd\mu\right)^{1/p}$$$$\inf\{r\in\bbR\mid\mu(\{x\mid |cf(x)|>r\})=0\}=|c|\inf\{r\in\bbR\mid\mu(\{x\mid |f(x)|>r\})=0\}$$
- Triangle Inequality: See lemma 2 for \(p\) finite. For \(p=\infty\), since for any \(x\), \(|f(x)+g(x)|\leq|f(x)|+|g(x)|\), we have $$\sup\limits_{x\in X}|f(x)+g(x)|\leq\sup\limits_{x\in X}|f(x)|+|g(x)|\leq\sup\limits_{x\in X}|f(x)|+\sup\limits_{x\in X}|g(x)|$$
Homogeneity also implies that \(\rmF^*\) is closed under scalar multiplication, and the triangle inequality implies that \(\rmF^*\) is closed under addition. This shows that \(\rmF^*\) is a vector space.
Thus, we apply the results of theorem 1 to generate a natural normed vector space with \(\Norm{}_p\) as the norm. We call this space \(L_p(\mu)\), \(L_p(X)\), or sometimes just \(L_p\) if the context is clear. We call \(\Norm{}_p\) the \(p\)-norm.I first claim that for any \(u,v\), $$e^{u/p+v/q}\leq\frac{e^u}p+\frac{e^v}q$$If \(p=\infty\), then this is true trivially. If \(p,q<\infty\), then letting \(t=\frac1p\in[0,1]\), we have $$e^{tu+(1-t)v}\leq te^u+(1-t)e^v$$which is true since \(e^x\) is convex.
If \(\Norm f_p=0\), then \(f\) is zero almost everywhere and thus, \(\Norm{fg}_1=0\). Thus, we can assume \(\Norm f_p,\Norm g_q\neq0\). Let \(F=f\cdot\Norm f_p^{-1}\) and \(G=g\cdot\Norm g_q^{-1}\). I claim that $$|F(x)G(x)|\leq\frac1p|F(x)|^p+\frac1q|G(x)|^q$$If \(F(x)=0,\infty\), the inequality is obvious true. If both \(|F(x)|,|G(x)|\) are positive, then let \(u,v\) be such that \(e^{u/p}=|F(x)|\), \(e^{v/q}=|G(x)|\). The previous inequality gives us this inequality. Thus, by monotonicity of integration, $$\Norm{FG}_1=\int|F(x)G(x)|d\mu\leq\frac1p\int|F(x)|^pd\mu+\frac1q\int|G(x)|^qd\mu$$$$=\frac1p\Norm F_p^p+\frac1q\Norm G_q^q$$$$=\frac1p+\frac1q=1$$This finishes the proof.If \(p=\infty\), note that if $$r\geq\inf\{a\in\bbR\mid\mu(\{x\mid |f(x)|>a\})=0\}+\inf\{a\in\bbR\mid\mu(\{x\mid |f(x)|>a\})=0\}$$then for any \(x\) such that \(|f(x)+g(x)|>r\), $$|f(x)|>\inf\{a\in\bbR\mid\mu(\{x\mid |f(x)|>a\})=0\}\text{ or }$$$$|g(x)|\geq\inf\{a\in\bbR\mid\mu(\{x\mid |g(x)|>a\})=0\}$$In either case, set of such \(x\) is a subset of a measure zero set, and thus has measure \(0\). This completes the proof.
If \(\Norm{f+g}_p=0\), this inequality is trivially true. So assume that \(\Norm{f+g}_p>0\). Since \(x^p\) is a convex function, we have \(\left(\frac{f+g}2\right)^p\leq\frac12(|f|^p+|g|^p)\). Integrating both sides tells us that \(\Norm{f+g}_p^{p-1}\) is finite (the \(p-1\) will become obvious later). Call this quantity \(M\).
Thus, we have $$\Norm{f+g}_p^p=\int|f(x)+g(x)|^{p-1}\cdot|f(x)+g(x)|d\mu$$$$\leq\int|f(x)+g(x)|^{p-1}\cdot|f(x)|d\mu+\int|f(x)+g(x)|^{p-1}\cdot|g(x)|d\mu$$Applying lemma 1 to both integrals, with \(\frac1p+\frac{p-1}p=1\), gives us$$\left(\Norm f_p+\Norm g_p\right)\cdot\left(\int|f(x)+g(x)|^{(p-1)\cdot(p/(p-1))}d\mu\right)^{(p-1)/p}$$$$=\left(\Norm f_p+\Norm g_p\right)\cdot M$$So our inequality is $$\Norm{f+g}_p^p\leq\left(\Norm f_p+\Norm g_p\right)\cdot M$$Since \(M\) is finite, we can divide both sides by \(M\) to get the desired result.It's important to note that the elements of \(L_p\) spaces are not functions. They are equivalence classes of functions. That being said, we'll often refer to functions as elements of \(L_p\) space, implicitly referring to the equivalence class the function represents.
Here are some interesting examples of \(L_p\) spaces:
- If \(X\) is the set \(\{1,\ldots,n\}\) for some \(n\in\bbN\), and \(\mu\) is the counting measure on \(X\), then observe that there is a vector space isomorphism between \(\bbR^n\) and the set of functions \(X\to\bbR\). Moreover, the \(L_p\) norm is distinguishable on \(\bbR^n\), meaning that the space \(L_p(\mu))\) is just \((\bbR^n,\Norm{}_p)\).
- If \(X\) is \(\bbN\) and \(\mu\) is again the counting measure, then there are some functions \(X\to\bbR\) that are not \(p\)-integrable. For example, the function \(f(x)=x\) is not \(p\)-integrable for any \(p\in[1,\infty]\).
- If \(X\) is a finitely measured subset of \(\bbR\), and \(\mu\) is the standard Lebesgue measure, then we have the following result: for all \(1\leq p< q\leq\infty\), \(L_q\subset L_p\). If \(q=\infty\), then for any \(f\in L_q\), there exists some \(M\in\bbR\) such that \(\card f\) is bounded above by \(M\) almost everywhere. Thus, $$\int|f|^pd\mu\leq\int M^pd\mu=|X|\cdot M^p$$Thus, \(f\in L_p\). If \(q<\infty\), then by lemma 1 applied to \(|f|^q=|f|^q\cdot 1\) with \(\frac qp+\frac{p-q}p=1\)$$\int|f|^qd\mu\leq\left(\int|f|^p\right)^{q/p}\left(\int 1^{p/(p-q)}d\mu\right)^{(p-q)/p}$$$$\int|f|^qd\mu\leq\Norm f_p^q$$To see that equality doesn't hold, consider \(X=[0,1]\), \(f(x)=x^{-1/q}\).
- If \(X\) is an infinitely measured subset of \(\bbR\) and \(\mu\) is the standard Lebesgue measure, we can't say much at all. For example, if \(X=[0,\infty)\), then the example from the previous bullet shows \(L_p\not\subset L_q\), and the function \(f(x)=x^{-2/p}\) shows \(L_q\not\subset L_p\).
Banach Spaces
Since normed vector spaces are also metric spaces, it seems natural to ask, are these metric spaces complete? Surprisingly, in the case of \(L_p\) spaces, the answer is yes!
However, this is not true generally. But, we can endow the completion of a normed vector space with a normed vector space structure, meaning that every normed vector space is isometrically embedded in a complete normed vector space. The proof of this is on page 17 here
Complete normed vector spaces are very useful, so much so that they have their own name: Banach spaces. The study of the properties of Banach spaces is better dealt with in a course on Functional Analysis, so I'll leave the discussion on these spaces here.
The following result will be one that we do use somewhat often.
Hilbert Spaces
Suppose we wanted a notion of an inner product in our normed vector space, i.e., a function that takes two vectors as input and outputs a scalar.
For starters, we'd want the inner product to be a bilinear mapping, meaning that it is linear on both inputs. And, we'd want the inner product of a vector with itself to be the square of the norm. This should make some intuitive sense when thinking about the dot product on real vector spaces, but you may ask why we'd want this condition in general. The answer, to be blunt, is just that these conditions are useful.
- Symmetry: \(x\cdot y=y\cdot x\)
- Linearity: \((x+y)\cdot z=x\cdot z+y\cdot z\) and \(cx\cdot y=c(x\cdot y)\).
- Norm: \(\Norm x^2=x\cdot x\)
A inner product space which is Banach is called a Hilbert Space. Which \(L_p\) spaces are Hilbert spaces?
We might hope that all of them are. For \(\bbR^n\), this is true. But for more complicated choices of \(X\), there is exactly one \(L_p\) Hilbert space. To see why, we'll use the following results, all proven here.
First, we show that the definition of the inner product is well defined. Observe that given \(f,g\in L_2\), \(\Norm f_2=\left(\int f^2d\mu\right)^{1/2}\) and similarly for \(g\). In other words, we can drop the absolute value bars. Thus, $$\Norm{f+g}_2^2=\int(f+g)^2d\mu=\int f^2d\mu+2\int fgd\mu+\int g^2d\mu$$In other words, we can define the inner product as $$f\cdot g=\frac12\left(\Norm{f+g}_2^2-\Norm f_2^2-\Norm g_2^2\right)$$This implies that the inner product is well defined.
Now to verify the properties of an inner product space.
- Symmetry: Obvious by the definition
- Linearity: Implied by the linearity of integration
- Norm: Obvious by the definition