Week 1 Notes
- Dimensional Analysis
- Number Bases
- Area and Circumference of the Circle
- Pythagorean Triples
- Permutations and Combinations
- Challenge: Distinguishability
Welcome to Advanced MB3! Click on any picture to expand it.
Dimensional Analysis
Our first topic for this class will be dimensional analysis. But what is dimensional analysis?
Dimensional analysis is the study of units (for example, kilogram, meter, celsius) and the tracking of these units as we do calculations.
As an example, we know that \(1\text{ inch }=2.54\text{ cm}\). So, if we want to convert \(6\) inches to centimeters, we can write the following: $$6\text{ in}\cdot\frac{2.54\text{ cm}}{1\text{ in}}=15.24\text{ cm}$$The idea here is to multiply by unit fractions, which are fractions that have value \(1\), since multiplying by \(1\) doesn't change the value.
Similarly, if I wanted to convert \(24\) centimeters into inches, I could apply the same idea, with the equation $$24\text{ cm}\cdot\frac{1\text{ in}}{2.54\text{ cm}}\sim9.45\text{ in}$$The golden rule is this: if I want to cancel out a unit that is in the numerator, I need to multiply by a fraction with the unit in the denominator. If I want to cancel out a unit in the denominator, I need to multiply by a fraction in the numerator. Remembering this golden rule should make dimensional analysis pretty simple.
Quiz
For the following problems, use the following table:| \(1\text{ mile}=5280\text{ ft}\) |
| \(1\text{ in}=2.54\text{ cm}\) |
| \(3\text{ feet}=1\text{ yard}\) |
| \(0.454\text{ kg}=1\text{ lb}\) |
| \(946\text{ mL}=1\text{ qt}\) |
| \(4\text{ qt}=1\text{ g}\) |
| \(12\text{ in}=1\text{ ft}\) |
| \(1\text{ min}=60\text{ sec}\) |
| \(1\text{ hr}=60\text{ min}\) |
| \(1\text{ day}=24\text{ hr}\) |
Number Bases
Our next topic is number bases. When I write the number \(245\), how do I understand what this number is?
We can separate it into digits. \(245=200+40+5\). Another way of writing this is$$245=2\cdot10^2+4\cdot10^1+5\cdot10^0$$What if we replaced \(10\) in the equation above by some other number \(b\)?
We call this numbers base \(b\). To write a number in base \(b\), we put a subscript \(b\) after the number to remind ourselves that this number is not in our normal way of writing it.
When we write number base \(b\), we use digits \(0,1,\ldots,b-1\). But what if \(b\gt10\). What digits do we use for numbers like \(10\) and \(11\)? Mathematicians usually use letters of the alphabet. \(A\) represents \(10\), \(B\) represents \(11\), and so on.
The most common base we use outside of our normal base \(10\) is base \(2\), which we call binary. It is very useful since we only need \(2\) digits: \(0\) and \(1\).
So how do we convert numbers in our normal base \(10\) to other bases? We use the greedy algorithm.
Circumference and area of the circle
The circle is one of the most fundamental geoemtrical objects we know, so finding the area and circumference of it is useful.
How do we find the circumference? The circumference formula tells us that a circle with radius \(r\) has circumference $$C=2\pi\cdot r$$In fact, \(\pi\) is defined as \(\frac C{2r}\). But this formula only works if \(C\) is proportional to \(r\). For example, if my circle's radius doubles, does the circumference also double?
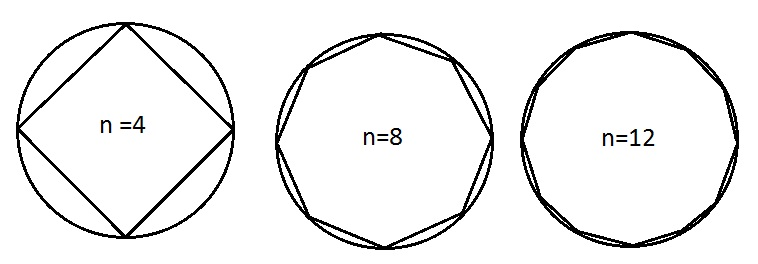
The answer is yes! To see why, remember that polygons with a lot of sides look very similar to circles. In the diagram below, the polygons circumscribe the circle, or equivalently, the circle is inscribed in each of them.
And when we double the side length of a regular polygon, the perimeter doubles too! And the circumference of the circle is very similar to the perimeter of the polygon with many sides.
So why is the area of the circle \(\pi r^2\)? Here's a cute little gif that shows why.
Pythagorean Triples
Now, let's talk about Pythagorean triples! Pythagorean triples are \(3\) integers \(a,b,c\) such that \(a^2+b^2=c^2\).
Pythagorean triples are special because they form right triangles! There exists a right triangle with legs \(a,b\) and hypotenuse \(c\).
Another way of thinking about Pythagorean triples is using the distance formula. The distance of a point \((x,y)\) from the origin is \(\sqrt{x^2+y^2}\). If \((x,y)\) satisfy \(x^2+y^2=z^2\), then \(z\) is the distance of the point from the origin! So Pythagorean triples are also sets of integer points in the plane that are an integer distance away from the origin.
But we can do something a bit more special with Pythagorean triples. Let's take the formula, and divide both sides by \(c^2\). We get $$\left(\frac ac\right)^2+\left(\frac bc\right)^2=1$$\(\frac ac,\frac bc\) are rational numbers, and \(\left(\frac ac,\frac bc\right)\) is on the unit circle.
If you are following along, what we have just realized is that Pythagorean triples are just like rational points on the unit circle. Now how do we find rational points on the unit circle?
Let \((p,q)\) be a rational point on the unit circle. Let's find the line that goes through the points \((p,q)\) and \((-1,0)\). This line is $$y=\frac{q+1}p(x+1)$$Note that this slope is rational! So, if we look at lines with rational slope going through \((-1,0)\), we will get our rational points on the unit circle.
So let us do that. Given slope \(\frac nm\), the line with this slope going through point \((-1,0)\) is $$y=\frac nm(x+1)$$And, the equation of the unit circle is $$x^2+y^2=1$$Substituting, we get $$x^2+\left(\frac nm(x+1)\right)^2=1$$$$\left(1+\frac{n^2}{m^2}\right)\cdot x^2+\left(\frac{2n^2}{m^2}\right)\cdot x+\frac{n^2}{m^2}-1=0$$$$\frac{m^2+n^2}{m^2}\cdot x^2+\frac{2n^2}{m^2}\cdot x+\frac{n^2-m^2}{m^2}=0$$$$(m^2+n^2)\cdot x^2+2n^2\cdot x+n^2-m^2=0$$We apply the quadratic formula to get $$x=\frac{-2n^2+2\sqrt{n^4-(n^4-m^4)}}{2(m^2+n^2)}=\frac{m^2-n^2}{m^2+n^2}$$$$y=\frac{2mn}{m^2+n^2}$$Thus, \(m^2-n^2,2mn,m^2+n^2\) is a Pythagorean triple, and in fact, every primitive (meaning with \(\gcd\) \(1\)) Pythagorean triple will have this form.
To see this concept in action, see the following Desmos graph. Set \(m,n\) to distinct integers and see how the corresponding right triangle looks!
Permutations and Combinations
The last topic for this week are permutations and combinations. What is the difference between the two?
In English, we use the word combination to mean a collection in which the order of things does not matter. For example:
- "My fruit salad consists of apples, bananas, and grapes": We don't care what order you put the fruit into the fruit salad. As long as it is well-mixed, the order does not matter.
- "The password is 54321": The value \(12345\) will not work as the password, even though it is just a rearrangement of the actual password. In this case, order of the digits matters.
In mathematics, when we want to count the number of ways to do things where order does not matter, we use combinations. If order does matter, we use permutations.
Permutations
There are two types of permutations
If I want to select \(k\) objects from \(n\) total objects, but I'm allowed to pick the same object multiple times, we call this permutation a permutation with replacement.
To come up with a formula for problems like the Example above, observe that for each object, there are \(n\) choices. So, the number of ways to select \(k\) objects from \(n\) is just $$\underbrace{n\times\ldots\times n}_{k\text{ times}}=\color{green}{n^k}$$
If I want to select \(k\) objects from \(n\) total objects, but I no longer can pick the same object twice, we call this permutation permutation without replacement.
To solve the example above, we realize that we have \(4\) different choices for the t-shirt, and then \(3\) choices for the pant, since one color is already taken by the t-shirt, and then \(2\) choices for the shoes since \(2\) colors are already taken. So, the number of permutations is \(4\times 3\times 2\). In general, if we want to pick \(k\) objects from \(n\) objects without replacement, there are \(n\times(n-1)\times\ldots\times(n-k+1)\) ways to do that.
That's an ugly formula. But, we can prettify it using factorials. For any number \(n\), the function \(n!\) gives us the product \(n\times(n-1)\times\ldots\times1\). So, our formula is $$_nP_k=\frac{n\times(n-1)\times\ldots\times1}{(n-k)\times(n-k-1)\times\ldots\times1}=\color{green}{\frac{n!}{(n-k)!}}$$
Combinations
Here too, there are two types of combinations.
If I'm not allowed to select the same object more than once, we call the problem combinations without replacements.
Combinations without replacement are very similar to permutations without replacement, except that order matters for permutations. In particular, let's consider our lottery example again.
- Permutations (Order matters): 123, 132, 213, 231, 312, 321
- Combinations (Order doesn't matter): 123
As we saw in the example, there are \(6\) times as many permutations as combinations, since for each potential combination, rearranging the combination gives us \(3!=6\) times as many permutations. In other words, to get the number of combinations without replacement, we divide \(_nP_k\) by \(k!\) to get $$_nC_k=\color{green}{\frac{n!}{k!(n-k)!}}$$
If we are allowed to select the same object multiple times, we call the problem combinations with replacement. This is the trickiest case, and doesn't show up very often on tests. Still, it is fun to analyze.
In this example, the order of the scoops doesn't matter, making it a combination, but I can also get the same flavor multiple times, which is why we need replacement.
To come up with a formula, we use a technique called stars and bars. For our example, stars and bars tells us that the answer is \(_3C_7\), and in general, we have $$_kC_{n+k-1}=\color{green}{\frac{(n+k-1)!}{k!(n-1)!}}$$
In summary, we have the following table:
| With Replacement | Without Replacement | |
| Permutations | \(n^k\) | \(\frac{n!}{(n-k)!}\) |
| Combinations | \(\frac{(n+k-1)!}{k!(n-1)!}\) | \(\frac{n!}{k!(n-k)!}\) |
Challenge: Distinguishability
Suppose I want to distribute \(n\) objects to \(k\) buckets. Simple, right? Well, not really. The answer depends on distinguishability of \(n\) and \(k\), or in other words, whether two objects are different or not.
Example of distinguishable \(n\) to distinguishable \(k\): Suppose I want to give away my book collection to the class. Assuming that each book is different, \(n\) is distinguishable, and people are always distinguishable, so \(k\) is also distinguishable.
You'll see plenty of problems that will require figuring out which of these \(4\) cases you are in, and then solving accordingly. Here is a table of the formulas for the \(4\) different cases.
| Distinguishable \(n\) | Indistinguishable \(n\) | |
| Distinguishable \(k\) | \(n^k\) | \(n+k-1\choose k-1\) |
| Indistinguishable \(k\) | Ugly Formula | No formula |
Unfortunately, two of the \(4\) cases do not have nice formulas in general. So if you run into either of these cases, you must solve with casework :( or use generating functions (not much better, to be honest)