Week 10 Notes
The examples in these notes have been developed by Daniel Velleman in his book How to Prove it
Deductive Reasoning
By this point, you've seen many proofs in this class, but what really is a proof? Intuitively, we think of proofs as a series of logical arguments. And by logical, we usually mean deductive reasoning.
Before explaining what deductive reasoning is, let's begin with a few examples.
- It will either rain or snow tomorrow
It's too warm to snow tomorrow
Therefore, it will rain tomorrow - I don't work on Sundays
Today is Sunday
Therefore, I don't work today - I will go to work today or tomorrow
I am not going to work today
I will go to work tomorrow
Each line in the examples above are called statements. Statements (for the most part) are either true or false. In the above examples, we took two statements as truth, and deduced a final statement as a consequence of the first two. We call the first two statements premises and the final statement a conclusion.
Which of the examples are most similar? On a cursory glance, you may think examples 2 and 3 are the most similar, as they both deal with going to work. But, in terms of the type of argument used, examples 1 and 3 are most similar. To see why, let's simplify the statements using variables.
Let \(R\) be the statement "It will rain tomorrow", \(S\) the statement "It will snow tomorrow", \(P\) the statement "I work today", \(Q\) the statement "I will work tomorrow", \(T\) the statement "I don't work on Sundays", and \(U\) the statement "Today is Sunday".
Thus, our examples are rewritten as follows:
- \(R\) or \(S\)
not \(S\)
Therefore, \(R\) - \(T\)
\(U\)
Therefore, not \(P\) - \(P\) or \(Q\)
not \(P\)
Therefore, \(Q\)
Once we've rewritten our examples with variables, the similarity between examples 1 and 3 becomes more clear. We know that at least one of two events will happens, and we know that a particular one doesn't happen, so the other must happen.
Using variables instead of english is advantageous because it allows us to see patterns that may be obscured by english, and it reduces the amount of characters needed to express an idea.
In fact, we can condense these statements even further, by establishing notation for or, not, and the other logical connectives.
| Name | Symbol |
|---|---|
| or | \(\vee\) |
| and | \(\wedge\) |
| not | \(\lnot\) |
| therefore | \(\therefore\) |
With these symbols, our third example becomes:
\(P\vee Q\)
\(\lnot P\)
\(\therefore Q\)
Either the cook or the maid has a child.
Either the doctor or the cook has a child
Therefore, either the doctor or the maid has a child.
Truth Tables
In the previous section, we converted our arguments to logical notation. But how do we check whether our arguments are correct or not? We use truth tables.
We want to make sure that regardless of whether each individual variable is true or not, the argument still holds. To do that, we make a truth table.
- \(P\) and \(Q\) are true
- \(P\) is true but \(Q\) isn't.
- \(Q\) is true but \(P\) isn't.
- Neither \(P\) nor \(Q\) are true
| \(P\) | \(Q\) | \(P\vee Q\) | \(\lnot P\) |
|---|---|---|---|
| T | T | T | F |
| T | F | T | F |
| F | T | T | T |
| F | F | F | T |
The technique above of using a truth table to verify an argument is very useful. To summarize, this is how to make and use a truth table.
- Given premises and a conclusion with \(n\) variables, make a table with \(2^n\) rows, each corresponding to the different permutations of true and false for the variables.
- Add columns for each of the premises and conclusion, and evaluate their truth value accordingly.
- Check to see whether there is a row where all of the premises are true and the conclusion is false.
If such a row exists, the argument is wrong. If it doesn't, the argument holds.
Either John is stupid, or John isn't stupid but just is lazy.
John is stupid.
Therefore, John isn't lazy
| \(S\) | \(L\) | \(\lnot S\vee L\) | \(S\vee(\lnot S\vee L)\) | \(\lnot L\) |
|---|---|---|---|---|
| T | T | T | T | F |
| T | F | F | T | T |
| F | T | T | T | F |
| F | F | T | T | T |
Logical Identities
While truth tables are an effective method of evaluating whether a logical argument is valid, it can get messy quite quickly. An statement with \(5\) variables will require \(32\) rows of a truth table.
Thus, we often employ logical identities to simplify otherwise complicated arguments into simpler ones. Here's a table of the identities you may want to remember.
| Identity | Statement | Simplification |
|---|---|---|
| Commutativity | \(P\vee Q\) | \(Q\vee P\) |
| \(P\wedge Q\) | \(Q\wedge P\) | |
| Associativity | \(P\vee (Q\vee R)\) | \((P\vee Q)\vee R\) |
| \(P\wedge (Q\wedge R)\) | \((P\wedge Q)\wedge R\) | |
| Idempotent | \(P\vee P\) | \(P\) |
| \(P\wedge P\) | \(P\) | |
| Distributive | \(P\vee (Q\wedge R)\) | \((P\vee Q)\wedge(P\vee R)\) |
| \(P\wedge (Q\vee R)\) | \((P\wedge Q)\vee (P\wedge R)\) | |
| Absorption | \(P\vee (P\wedge Q)\) | \(P\) |
| \(P\wedge(P\vee Q)\) | \(P\) | |
| De Morgan | \(\lnot(P\vee Q)\) | \(\lnot P\wedge\lnot Q\) |
| \(\lnot(P\wedge Q)\) | \(\lnot P\vee\lnot Q\) | |
| Double Negation | \(\lnot\lnot P\) | \(P\) |
Quantifiers
Sometimes, we run into formulas, which are statements, but with certain variables. Given a choice of value for those variables, the statement becomes one whose truth value we can evaluate.
Here's a silly example: consider the formula "\(x\) is an even number". The truth value of this formula depends on the value of \(x\). If \(x=0\), it is false. If \(x=1\), it is true. If \(x\) is a person, it is false.
We often write formulas as \(P(x)\), where \(x\) is the variable in the formula. Formulas can have multiple variables, in which case we'd write \(P(x_1,\ldots,x_n)\).
How do we turn formulas into statements? We use quantifiers.
As you can see in the example above, the \(forall\) symbol allows us to pick a domain of values for a variable, and ask the question, "for every \(x\) in our domain, is the resulting statement true?".
Similarly, we have another quantifier.
The example above introduces the other common quantifier, known as the Existential Quantifier. These two quantifiers are widespread throughout mathematics.
Challenge: Model Theory
Knowledge of induction is a prerequisite for this section, so unless you are familiar with it, I'd suggest reading Week 12's notes prior to this section.
Counting
The ability to count is one of the first skills we look for young children to grasp, but it often is forgotten how difficult a task this is.
Zvonkin points to the following example. Let's step into the child's shoes and learn how to count, but in Japanese.
ichi, ni, san, shi, go, roku, shichi, hachi, kyu, ju
First, you have to memorize these names. It is not easy! Once you've done this, now you have to learn to count backwards. ju, kyu, hachi,... Once you have done this, try to do some basic arithmetic. What is ichi plus roku? Hachi divided by shi?
Over time, though, we begin to forget how difficult the task of counting is. It is natural, we think. Why is \(1+1=2\)? What else would it be? After all, if I put one apple and another apple together, of course I get two apples!
But we, as logicians, shouldn't be satisfied by this non-answer. After all, logic is the study of conclusions following from statements. From what statement does \(1+1=2\) follow?
But even an answer to this question wouldn't feel particularly satisfactory. I could say, \(1+1=2\) due to the rules of arithmetic, made precise by the logicians before me. But \(1+1=2\) doesn't feel that way.
Figuring out facts about the natural numbers doesn't feel like we are deducing conclusions from assumptions. It feels like we are discovering these numbers, and we have invented rules to describe them. The natural numbers, in some fashion, are baked into the universe. So what are they? Are numbers real? Inventions? Logical? Physical?
Models
In logic, we view the notion of \(1\) apple and \(1\) apple forming \(2\) apples to be a model, a representation of a rule. \(1+1=2\) is a rule which informs us about how objects behave, and the apples are a representation of it.
But this, too, isn't the full picture, since the natural numbers themselves are a model. But of what?
To answer this question, let's play a little game. Suppose I am a logician from another land, one where the ideas of the natural numbers aren't known. How exactly would you explain to me what they are?
You could try showing me the apples, but that'd be of little use. As with the children learning to count, what gives meaning to the abstraction of apples combining to arithmetic is the idea that addition generalizes, and applies to all objects, not just apples.
You may also try to get me to look at my fingers (if I have them), and teach me to count this way. But this would be a bit like teaching you the words ichi, ni, san, ... I would immediately understand that these words serve a function for you, but have little perspective as to what function.
The best approach would be to set up rules. We'd hope to develop rules so that any model of these rules must behave intuitively like the natural numbers do. So where do we start?
Perhaps we'd start with \(0\). You might inform the logician, there exists a special natural number, and we call it zero.
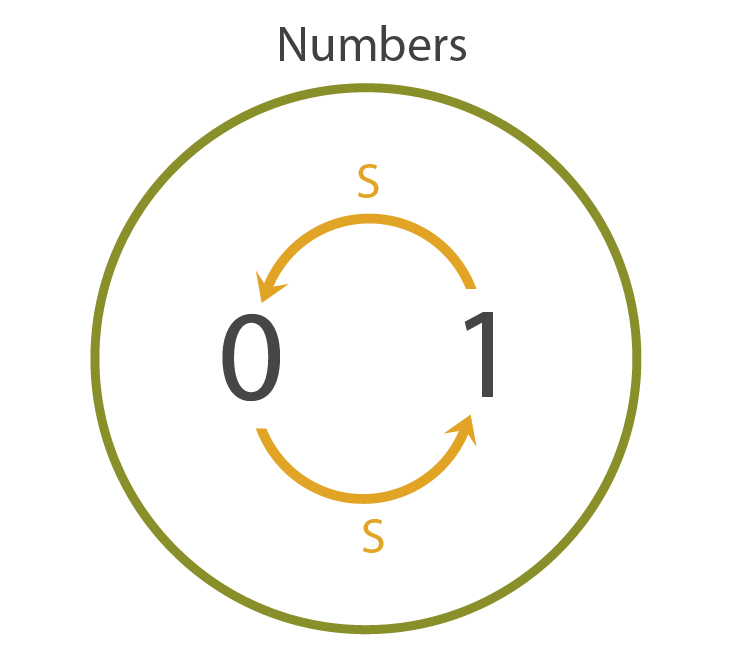
Next, we'd introduce the idea of a successor. For us normal folk, the successor of a natural number is just the number \(+1\), but since we haven't even gotten around to addition yet, we'll use this idea instead. To represent the successor of a number \(n\), we will write \(Sn\).
This is all of the notation we need to write our rules. The first rule, simple as it sounds, is just "0 is a natural number".
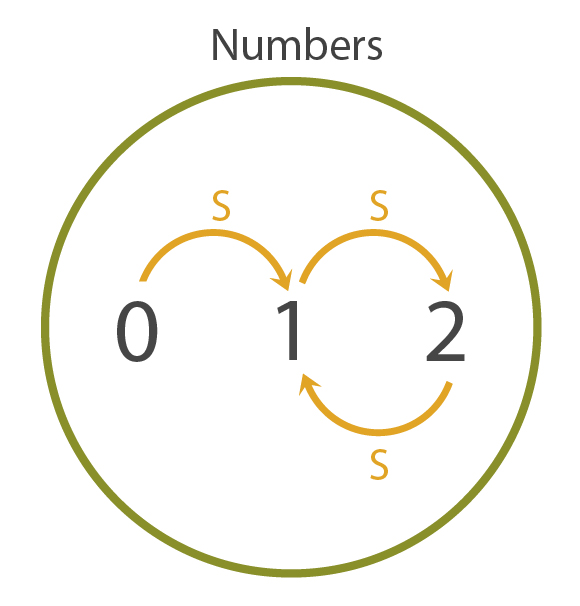
The second rule, as you may guess, is "every natural number has a successor". You may think these two rules are sufficient, but our alien friend presents us a model of our rules which puts that belief into question.
In our friend's model, \(1\) is the successor of \(0\), and \(0\) is the successor of \(1\). That, of course, isn't a model we want to allow, so we introduce a new rule: "No natural number has \(0\) as a successor". But this, too, isn't good enough. Our alien friend presents a revised model.
In this model, no number has \(0\) as a successor, but that doesn't prevent the looping behavior we'd like to avoid. So what rule can we introduce to avoid it?
The rule we are looking for is injectivity. In other words, if for any two natural numbers \(x,y\), if \(Sx=Sy\), then \(x=y\). This ensures that \(Sx\) maps to new numbers, avoiding the loop. Right? Well, kind of.
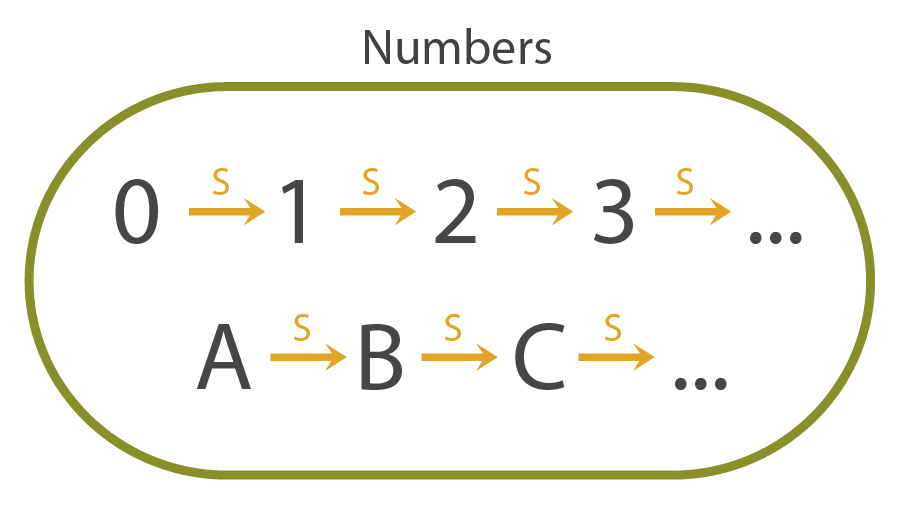
Our friend presents a revised model which fits with our new rule set. In this model, we do get the infinite chain behavior we expect from the naturals, but we also have a secondary chain, which is undesirable. So how do we fix this? We can modify our second rule to be: "0 is the only natural number which is not the successor of any natural".
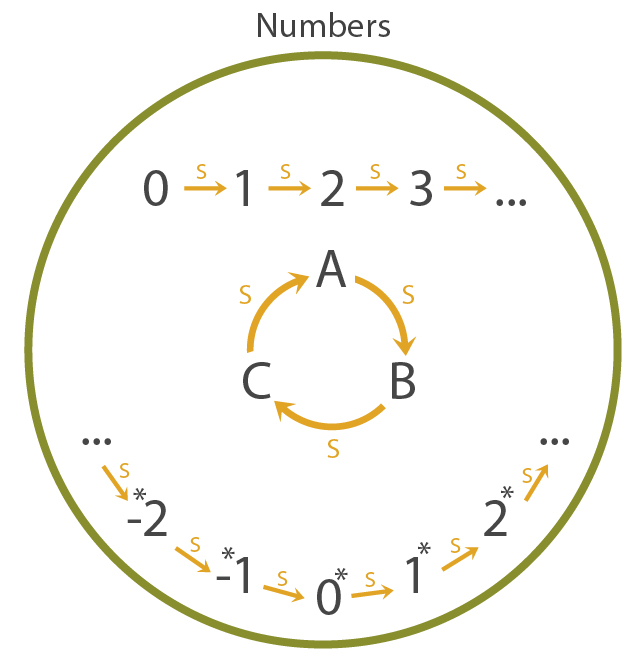
But even this isn't sufficient. Our alien friend presents yet another model of the natural numbers that looks nothing like what we think of the natural numbers.
Clearly, in the model above, there is a \(0\) element, it is the only element without a successor, and successorship is injective.
At this point, you are frustrated. No matter what rules you try, you aren't able to prevent our alien friend from coming up with a model of the rules different from your intuition of the numbers. So what is going on?
Logical Order
Let's attempt to write up the rules we've come up with so far. Our logical language has two symbols: \(0\) and \(S\), with symbols like \(1,2,\ldots\) as notation for \(S0,SS0,\ldots\).
Our first rule is that there exists a \(0\) element. We write that as follows: $$\exists x\in\mathbb N,\;x=0$$
Our second rule is that \(0\) is the only element that isn't the successor of any element. This is a bit messy to write out, but it would look like this: $$\left(\forall x\in\mathbb N,\;Sx\neq0\right)\wedge\left(\forall x\neq0\in\mathbb N\;\exists y\in\mathbb N,\;x=Sy\right)$$
Our third rule is injectivity. We'd write it as follows:$$\forall x,y\in\mathbb N,\;Sx=Sy\to x=y$$As a brief side note, the symbol \(\to\) represents "implies". In other words, \(A\to B\) is true if it is not true that \(A\) is true and \(B\) is false.
So why have we written these rules in logical notation? Well, so we can distinguish the different orders of logic. Any logical statement that doesn't use quantifiers is considered to be part of propositional logic, otherwise known as \(0\)th order logic.
First order logic contains all of \(0\)th order logic, but also allows for quantifiers over the model. In our case, we are modelling the natural numbers, so we can quantify over them using \(\forall\) and \(\exists\).
As you can tell, all three of our rules have been written in first order logic. Are there any other forms of logic?
The answer is yes!
What if we wanted to quantify not over the natural numbers, but over first order formulas! We can do this, and we call this sort of logic second order logic. If you are confused, let's do an example.
To write this in logical notation, we need to know what exactly \(P\) is. In fact, \(P\) is just a single-variable first-order logical formula! So we can write as follows: $$\forall\text{ first order formulas }P(x)\left(P(0)\wedge\forall n\in\mathbb N,\;P(x)\to P(x+1)\right)\to\forall n\in\mathbb N,\;P(n)$$This second order statement is the principle of mathematical induction.
You can start to guess at what third order, fourth order, and even \(n\)th order logic looks like.
Induction
Let's return to our game with our newly discovered second order logic. How do we rule out our alien friend's model of the natural numbers? Intuitively, we want to say that all of the natural numbers should be "connected" to \(0\), or in other words, if I add one to \(0\) sufficiently many times, I should be able to reach any natural number.
But we already have found a way of saying this! The final rule that we need is induction! Why does induction do the job?
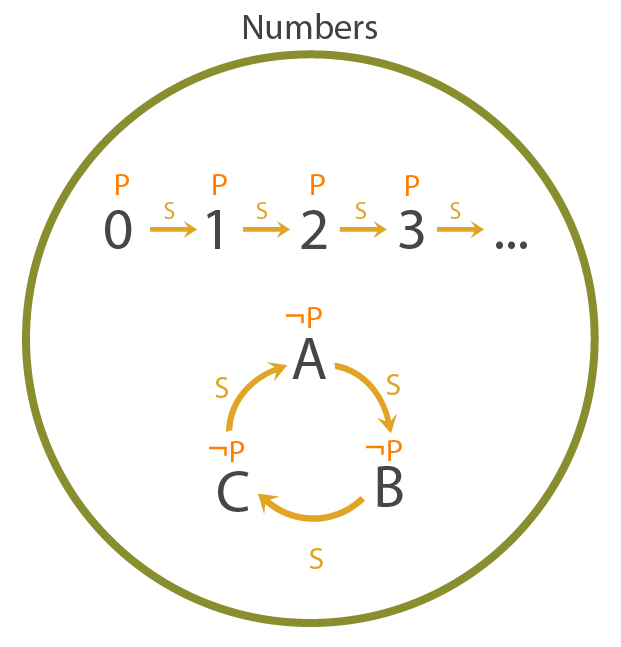
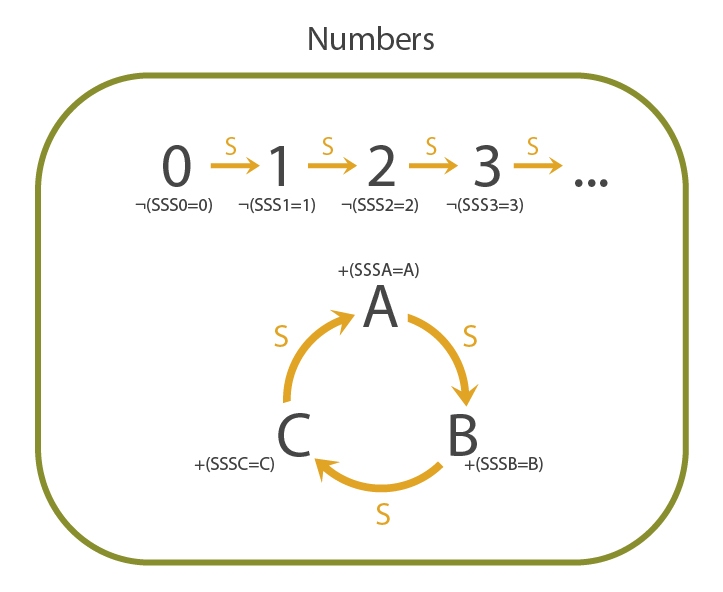
For any non-natural number, we can find some property \(P\) that satisfies the natural numbers, but doesn't satisfy the non-natural number, which we call non-standard numbers.
A property which does this for the \(3\) element loop \(A-B-C\) is the following:
That's awesome! So our final ruleset is as follows:
- \(\exists x\in\mathbb N,\;x=0\)
- \(\left(\forall x\in\mathbb N,\;Sx\neq0\right)\wedge\left(\forall x\neq0\in\mathbb N\;\exists y\in\mathbb N,\;x=Sy\right)\)
- \(\forall x,y\in\mathbb N,\;Sx=Sy\to x=y\)
- \(\forall\text{ first order formulas }P(x)\left(P(0)\wedge\forall n\in\mathbb N,\;P(x)\to P(x+1)\right)\to\forall n\in\mathbb N,\;P(n)\)
So to answer our initial question, these \(4\) rules are the rules whose model is the natural numbers we are used to.
Consistency
Before we celebrate too much, there are still some considerations to be had. First, how do we know that there isn't some other weird model that our alien friend can think of that violates our rule set? Perhaps more troublingly, what if these rules are contradictory?
Some of our concerns can be resolved by the following theorem.
This is great, since we have a model for our rules! This means that our rules are consistent! Well, almost. We'll only really described our models with nice pictures. To really establish the existence of a model, we'd have to build the natural numbers from scratch, which requires set theory (and we won't touch that for now).
An alternate approach is to drop the \(4\)th rule of the natural numbers. With this, we can apply the above theorem to generate ourselves a model! Will it be a model of the natural numbers as we know them? Not necessarily: there might be non-standard numbers in there. But, there are ways of dealing with these numbers.
Non-Standard Models
For now, we'll resort to the second approach, since set theory is a no-go (for now). So how do we know that there even exists non-standard models? We invoke the next theorem.
We'll use it as follows. We'll take our \(3\) natural number rules, and add a new symbol \(\infty\). And, we add the following rules: $$\infty\gt0$$$$\infty\gt1$$$$\vdots$$
For any finite subset of these rules, we have finitely many of these \(\infty\gt k\) rules. Call them \(\infty\gt k_1\), \(\infty\gt k_2\), ..., \(\infty\gt k_n\). Let \(x = \max(k_1,\ldots,k_n)+1\). So, \(x\gt k_1\), \(x\gt k_2\), etc, and thus the natural numbers satisfies this rule set!
By the compactness theorem, there exists a number \(\infty\) that is bigger than any natural number in a valid model of the natural numbers. This tells us that there are non-standard models.
This is only the tip of the iceberg: much of logic is playing around with fun non-standard models to prove interesting things!