\ie\cf
\newcommand{\eqdef}{\mathbin{\stackrel{\rm def}{=}}}  \newcommand{\R} % real numbers  \newcommand{\N}} % natural numbers  \newcommand{\Z} % integers  \newcommand{\F} % a field  \newcommand{\Q} % the rationals  \newcommand{\C}{\mathbb{C}} % the complexes  \newcommand{\poly}}  \newcommand{\polylog}}  \newcommand{\loglog}}}  \newcommand{\zo}{\{0,1\}}  \newcommand{\suchthat}  \newcommand{\pr}[1]{\Pr\left[#1\right]}  \newcommand{\deffont}{\em}  \newcommand{\getsr}{\mathbin{\stackrel{\mbox{\tiny R}}{\gets}}}  \newcommand{\Exp}{\mathop{\mathrm E}\displaylimits} % expectation  \newcommand{\Var}{\mathop{\mathrm Var}\displaylimits} % variance  \newcommand{\xor}{\oplus}  \newcommand{\GF}{\mathrm{GF}}  \newcommand{\eps}{\varepsilon}  \notag
\no
Back to MB3

Week 14 Notes

100%

In this week, we'll take a look at exponents and logarithms, and learn how to manipulate them to our advantage.

Exponential Functions

There is a classic tale in Indian folklore that goes like this: a wise man, when asked by the king to declare what he wants as a reward, said that he wants a chessboard full of rice. On the first square, he wants \(1\) grain. On the second square, he wants \(2\) grains. And on the \(n\)th square, he wants \(2\) times as many grains as on the previous square.

When the king heard this request, he laughed, thinking that the wise man was a fool for making such a simple request. But after he commanded his servants to return with the chessboard, he soon realized his folly. The final square would require \(2^{63}\) grains of rice: more grains then there are grains of sand on the entirety of Earth.

Exponential functions are deceiving because they grow amazingly fast. In fact, they grow faster than any polynomial function can. But what are exponential functions?

Repeated Multiplication

When we first learn about exponents, we learn about them as repeated multiplication. In other words, $$a^b=\underbrace{a\cdot a\cdot\ldots\cdot a}_{b\text{ times}}$$However, this definition doesn't work for other types of exponents. What if \(b\) is a rational number? What if \(b\) is a real number? What if \(b\) is complex? In this section, we'll redefine exponents to be more general.

Interest

Suppose I had \(\$100\), and I wanted to invest the money in a bank to earn interest. I have two deals available to me.

Which deal should I take?

Let's do the math.

So, Bank B is offering the sweeter deal.

Another way to think about it is this: when Bank A offers \(100\%\) interest, that's the same as them paying \(\$50\) twice in the year. But Bank \(B\) initially pays us \(\$100\cdot0.5=\$50\), but on the second interest payment, the \(50\%\) is applied to \(\$150\), rather than \(\$100\), leading us to have more money in the Bank.

So what happens if Bank C provides \(25\%\) interest every \(3\) months? Or Bank D provides \(10\%\) interest \(10\) times a year? How can we compare such deals?

Suppose some Bank offers \(\frac{100\%}n\) interest \(n\) times a year. In that case, your principal investment of \(\$100\) will be increased by \(\frac1n\) of the total \(n\) times. In other words, the final amount is $$\$100\cdot\left(1+\frac1n\right)^n$$With this formula, we can compare the different interest models of our banks.

Frequency Formula Final Amount
Annually\(\$100\cdot(1+1)^1\)\(\$200\)
Semi-annually\(\$100\cdot\left(1+\frac12\right)^2\)\(\$225\)
Quarterly\(\$100\cdot\left(1+\frac14\right)^4\)\(\$244.14\)
Monthly\(\$100\cdot\left(1+\frac1{12}\right)^{12}\)\(\$261.30\)
Daily\(\$100\cdot\left(1+\frac1{365}\right)^{365}\)\(\$271.46\)
Hourly\(\$100\cdot\left(1+\frac1{8760}\right)^{8760}\)\(\$271.81\)
Per Minute\(\$100\cdot\left(1+\frac1{525600}\right)^{525600}\)\(\$271.83\)
Per Second\(\$100\cdot\left(1+\frac1{31536000}\right)^{31536000}\)\(\$271.83\)

Interestingly, while the final amount increases as the frequency of interest payments increases, it seems to be converging upon a number. In fact, we have a name for this phenomenon: a limit. We write our observation as follows:$$\lim\limits_{n\to\infty}\$100\cdot\left(1+\frac1n\right)^n\sim\$271.83$$

This limit is such an important limit that we give it a name: \(e\). We define \(e\) as follows:$$e=\lim\limits_{n\to\infty}\left(1+\frac1n\right)^n$$\(e\) is approximately \(2.71828\).

Now, we can define continuous interest. We get interest "infinitely often" at an "infinitesimal rate". The formula for the amount of money received is the following:$$Pe^{rt}$$

In other words, we've ended up with a formula in terms of \(e^x\). But that gets us no closer to defining exponentiation. How do we evaluate this?

Natural Exponentiation

Luckily for us, there's an alternate formula for \(e^x\) besides the limit one.

For any complex \(x\), the following formula holds$$\lim\limits_{n\to\infty}\left(1+\frac xn\right)^n=\sum\limits_{n=0}^\infty\frac{x^n}{n!}$$


Using the Binomial Theorem from Week 3, $$\left(1+\frac xn\right)^n=1+\frac n{1!}\cdot\frac xn+\frac{n(n-1)}{2!}\cdot\frac{x^2}{n^2}+\frac{n(n-1)(n-2)}{3!}\cdot\frac{x^3}{n^3}+\ldots+\frac{x^n}{n^n}$$When \(n\) gets large, this expression approaches $$1+\frac {xn}n+\frac{x^2n^2}{2!\cdot n^2}+\frac{x^3n^3}{3!\cdot n^3}+\ldots$$To actually prove this, we'd have to use the definition of limits, which is outside the scope of this class.

Letting \(x=1\), we have a formula for \(e\) that doesn't require taking a limit. That's a step in the right direction, but it doesn't help us evaluate \(e^x\). Or does it?

In fact, without realizing it, we've just defined \(e^x\).

We define \(e^x\) as $$e^x=\lim\limits_{n\to\infty}\left(1+\frac xn\right)^n=\sum\limits_{n=0}^\infty\frac{x^n}{n!}$$

To see that this definition is in fact the exponentation we are used to, let's prove some basic properties.

For all complex \(x,y\), \(e^{x+y}=e^x\cdot e^y\).


We'll use the \(\sum\limits_{n=0}^\infty\frac{x^n}{n!}\) definition for this proof. If we show that for any natural number \(i,j\), the coefficient of \(x^iy^j\) in \(e^{x+y}\) and \(e^xe^y\) are the same, then we are done.


In \(e^{x+y}\), the term \(x^iy^j\) is part of the term \(\frac{(x+y)^{i+j}}{(i+j)!}\). So, the term, via the Binomial Theorem, is $${i+j\choose i}\cdot\frac{x^iy^j}{(i+j)!}=\frac{x^iy^j}{i!j!}$$In \(e^xe^y\), the term \(x^iy^j\) comes from the product of the terms \(\frac{x^i}{i!}\) and \(\frac{y^j}{j!}\), giving us \(\frac{x^iy^j}{i!j!}\). This completes the proof.
Using the summation definition of \(e^x\) and the above theorem, show the following facts:
  • \(e^0=1\)
  • For all \(x\gt0\), \(e^x\gt1\)
  • For all real \(x\), \(e^x\gt0\)

This theorem shows that \(e^n=\underbrace{e\cdot e\cdot\ldots\cdot e}_{n\text{ times}}\) for natural \(n\).

Logarithmic Functions

We now have a general definition of exponentiation, but there are several issues. One, we only defined exponentiation when \(e\) is the base. What about other bases? Also, given exponential equations like \(e^x=5\), how do we find the solution? To both of these questions, and many more, logarithms are the solution.

Given a positive real \(x\), we define the natural logarithm of \(x\), denoted by \(\ln x\) or sometimes just \(\log x\), the real number such that $$e^{\ln x}=x$$

The logarithm should be viewed as almost an inverse function to the exponential function. By that logic, you'd expect the log function to grow very slowly, which it does!

But there's an issue: How do we know that the log function even exists? How do we know that there is a unique \(\ln x\) such that \(e^{\ln x}=x\)?

For any positive \(x\), there exists a unique real \(\ln x\) such that \(e^{\ln x}=x\).


Uniqueness: \(e^x\gt0\) for all real \(x\), as shown in an exercise above. Thus, for any real \(x,y\) such that \(x\neq y\), then \(y\gt x\) or \(x\gt y\). Assume \(y\gt x\), since the other case is identical (just switch the variable names). Then, \(y-x\gt0\), so \(e^{y-x}\gt0\) and $$e^y=e^xe^{y-x}\gt e^x$$So, there can only be one real solution to the equation \(e^x=z\).


Existence: We want to find a real number \(\ln x\) such that \(e^{\ln x}=x\). Let's first show that for any real \(t\) and natural number \(n\) satisfying \(n\gt\frac{e-1}{t-1}\), \(e^{1/n}\lt t\). To see why, note that \(e^{1/n}\gt1\), so by the geometric series formula$$n=\sum\limits_{k=0}^{n-1}1\lt\sum\limits_{k=0}^{n-1}\left(e^{1/n}\right)^k=\frac{\left(e^{1/n}\right)^n-1}{e^{1/n}-1}$$Rewriting the inequality gives us \(e-1\gt n\left(e^{1/n}-1\right)\). Since \(n\gt\frac{e-1}{t-1}\), \(t\gt e^{1/n}\).

This implies that for any real \(w\) such that \(e^w\gt x\), letting \(t=x^{-1}e^w\gt1\) gives us \(e^{1/n}\gt e^wx^{-1}\) for \(n\gt\frac{e-1}{t-1}\), so $$e^{w-\frac1n}\gt x$$So, define \(\ln x\) as the smallest number such that \(e^w\not\lt x\). If \(e^{\ln x}\gt x\), then for some natural number \(n\) as we saw earlier, \(e^{\ln x-\frac1n}\gt x\), which is a contradiction since \(\ln x\) is the smallest real number such that \(e^{\ln x}\not\lt x\). So, it must be the case that \(e^{\ln x}=x\).

The above proof is quite wordy, but with it, we are now able to take logarithms. Our first order of business is to define exponentiation by alternate bases.

For any positive real \(a\) and complex \(b\), we define $$a^b=e^{b\ln a}$$

This definition may not make a lot of sense, until you see the following theorems.

For any real \(x\) and complex \(y\), \(e^{xy}=\left(e^x\right)^y\).


$$\left(e^x\right)^y=e^{y\ln(e^x)}$$Note that the number \(z\) such that \(e^z=e^x\) is just \(x\), we have \(\ln(e^x)=x\). This completes the theorem.
For all complex numbers \(x,y\), \(a^{x+y}=a^xa^y\).


$$a^{x+y}=e^{\ln a\cdot x+\ln a\cdot y}=e^{\ln a\cdot x}e^{\ln a\cdot y}=a^xa^y$$

With theses theorem, \(e^{b\ln a}=\left(e^{\ln a}\right)^b=a^b\). We now have a way of defining logarithms with arbitrary bases. Now, what about alternate bases for logs?

Given positive real numbers \(a,b\), note that $$a^{\frac{\ln b}{\ln a}}=\left(a^{\frac1{\ln a}}\right)^{\ln b}=\left(e^{\frac{\ln a}{\ln a}}\right)^{\ln b}=e^{\ln b}=b$$So, we define \(\log_ab\), the number for which \(a^{\log_ab}=b\), as $$\log_ab=\frac{\ln b}{\ln a}$$

We can now prove a bunch of useful properties for logarithms.

Given positive reals \(a,b,c\) and real number \(x\), the following equations hold:$$\log_ab=\frac{\log_cb}{\log_ca}\tag{1}$$$$\log_ab+\log_ac=\log_a(bc)\tag{2}$$$$\log_ab^x=x\log_ab\tag{3}$$$$\log_a1=0\tag{4}$$


$$a^{\frac{\log_cb}{\log_ca}}=e^{\frac{\log_cb\ln a}{\log_ca}}=e^{\frac{\ln a\ln b\ln c}{\ln a\ln c}}=e^{\ln b}=b$$$$a^{\log_ab+\log_ac}=a^{\log_ab}a^{\log_ac}=bc$$$$a^{x\log_ab}=e^{x\ln a\cdot\frac{\ln b}{\ln a}}=e^{x\ln b}=b^x$$$$a^0=1$$
Back in the day when calculators weren't widely available, computing the product of large numbers was quite tedious. However, accountants soon realized equation \((2)\) could help them simplify the computation. Soon, accountants would print large books full of logarithms for the purpose of multiplying numbers. The process looks like this
  • Given \(x,y\), find \(\ln |x|,\;\ln |y|\) in the log table.
  • Compute \(\ln|x|+\ln|y|\)
  • Find \(\ln|x|+\ln|y|\) in the exponent table
Even up till as recently as the 1990s, log tables were omnipresent in businesses around the world.

Applying Logarithms

Both exponents and logarithms are extremely useful in mathematics. Of course, we can't cover all of their applications here, but here are a few interesting ones.

The prime number theorem answers the question: "Approximately how many primes are there less than \(N\)" for any \(N\). If we let \(\pi(n)\) be the number of primes \(\leq n\), then the prime number theorem tells us the following:$$\lim\limits_{n\to\infty}\frac{\pi(n)\ln n}n=1$$In other words, the ratio between \(\pi(n)\) and \(\frac n{\ln n}\) approaches \(1\) as \(n\) becomes very big. This result is quite powerful since it essentially tells us that for a large natural \(n\), the probability of a randomly chosen natural less than \(n\) being prime is \(\frac1{\ln n}\).

The proof of this theorem unfortunately requires complex analysis, but Chebyshev proved a weaker version of the Prime Number Theorem back in 1850 that only uses the Binomial theorem! See that proof here.

Another fun application is the following equation:$$\ln 2=1-\frac12+\frac13-\frac14+\ldots$$Logarithms will show up in many places, so it's worth getting to know them well.

Challenge: Complex Logarithms

So far, we've only defined \(\ln\) to take positive real numbers as inputs. But what about more general inputs? Can we define such a \(\ln\) function?

Let's state our problem more precisely. Given some complex number \(z\neq0\), we want to solve the equation \(e^w=z\) for complex \(w\).

Letting \(z=re^{i\theta}\) using the polar form presented in Week 7, and \(w=a+bi\), we get$$e^ae^{bi}=re^{i\theta}$$Two complex numbers are equal with at least one nonzero if and only if their magnitudes (i.e., distance from the origin) are the same, and their arguments (angle made with positive \(x\)-axis) are also the same. Since the magnitude of the left side of the equation is \(e^a\), and the argument is \(b\), while the magnitude of the right side is \(r\) and the argument is \(\theta\), we have \(r=e^a\) and \(b=\theta+2\pi k\) for some integer \(k\). We add the \(2\pi k\) term since rotating by \(2\pi\) has no effect on the argument of a complex number (since \(2\pi\) radians is \(360^\circ\)).

Thus, \(a=\ln r\), so $$w=\ln r+i(\theta+2\pi k)$$But this is an issue! There is more than one \(w\) satisfying the equation.

Because of this, we call the logarithm over the complex numbers a multi-valued function, since there are multiple valid values of \(\ln z\) for any non-zero \(z\).

We define the \(k\)th branch of the log function, written as \(^k\ln z\), as follows:$$^k\ln re^{i\theta}=\ln r+i\theta+2\pi ik$$We call the \(0\)th branch the principal branch of the logarithm.

With branching, we can pick which output we want from the logarithm function.

Given \(z=-1-\sqrt3i\), \(r=\sqrt{1^2+\sqrt3^2}=2\), and \(\theta=-\tan\frac{-\sqrt3}{-1}=-\frac{2\pi}3\). So, $$^k\ln z=\ln 2-\frac{2\pi i}3+2\pi ik$$
With our new definition of \(\ln\), we can now use our definition of \(\log_ab\) to define it for any complex \(a,b\) as long as \(b\neq0\). However, the choice of branch does influence the value of \(\log_ab\), so be careful when using such logs.

Roots of Unity

Let's use our complex logarithms to solve the following equation:$$x^n=z$$for complex \(x,z\neq0\), and natural \(n\).

Letting \(z=re^{i\theta}\), we have $$x^n=re^{i\theta}$$Thus, if we let \(y=\sqrt[n]r\cdot e^{i\frac\theta n}\), then \(y^n=r\cdot\left(e^{i\frac\theta n}\right)^n=z\). Thus, \(y\) is a solution to our equation.

But it isn't the only one. How do we find the others? Well, suppose \(\zeta\) is a solution to the similar equation \(x^n=1\). Then, for any natural number \(k\), $$(\zeta^ky)^n=(\zeta^n)^k\cdot y^n=re^{i\theta}$$Thus, \(\zeta^ky\) is another solution to our equation!

And, if \(y\) and \(y_*\) are both solutions to \(x^n=re^{i\theta}\), then $$\left(\frac y{y_*}\right)^n=\frac{y^n}{y_*^n}=1$$In other words, \(\frac y{y_*}\) is a solution to \(x^n=1\).

To summarize, if we can find the solutions to \(x^n=1\), by multiplying each of them by \(\sqrt[n]r\) and rotating them by \(\frac\theta n\), we have found all of the solutions to \(x^n=re^{i\theta}\). We call the solutions to \(x^n=1\) the roots of unity.

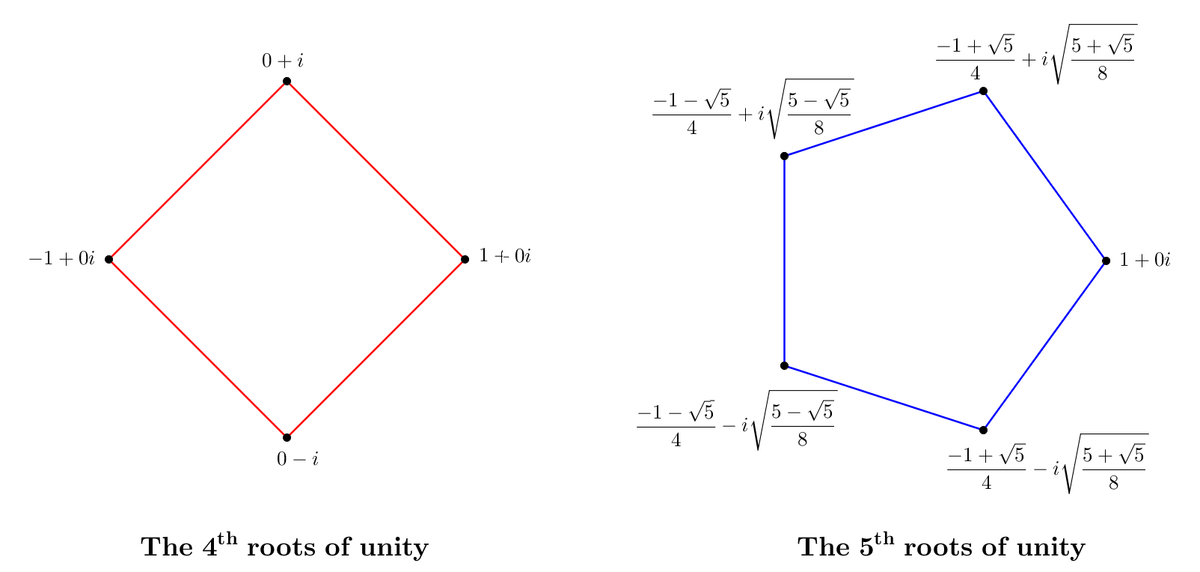
So what are the roots of unity? The first root of unity is obvious: \(1\). \(1\) always is a solution to \(x^n=1\) no matter the value of \(n\). To find the others, let's use the definition of exponentiation.

$$e^{n\ln x}=e^0\to n\ln x=2\pi ik\to x=e^{\frac{2\pi ik}n}$$In other words, the \(n\)th roots of unity are just the points in the complex plane that you get from rotating \(1+0i\) counterclockwise by \(\frac{360^\circ}n\) degrees. For example, here are the \(4\)th and \(5\)th degrees of unity.

Roots of unity always form a regular polygon, since all of the central angles are \(\frac{2\pi}n\). What other special properties do the roots of unity have?

For starters, they can all be generated by taking powers of one root of unity. Note that the roots of unity are \(e^{\frac{2\pi ik}n}\) for \(0\leq k\lt n\), and $$(e^{\frac{2\pi i}n})^k=e^{\frac{2\pi ik}n}$$We call \(\zeta=e^{\frac{2\pi i}n}\) the primitive \(n\)th root of unity, as it generates the other roots of unity.

Thus, we have the following equation for any natural \(n\):$$1+x+x^2+\ldots+x^{n-1}=\frac{x^n-1}{x-1}=\prod\limits_{k=1}^{n-1}\left(x-\zeta^k\right)$$

If \(\gamma\neq1\) is a \(n\)th root of unity, $$S=1+\gamma+\ldots+\gamma^{n-1}=0$$


$$\gamma S=\gamma+\gamma^2+\ldots+\gamma^{n-1}+\gamma^n=\gamma+\gamma^2+\ldots+\gamma^{n-1}+1=S$$$$(\gamma-1)S=0$$Since \(\gamma\neq1\), \(S=0\).

Can you prove this via Vieta's Formulas instead? What other interesting facts can you prove using Vieta's formulas applied to the polynomial \(1+x+\ldots+x^{n-1}\)?

As a final interesting application, occasionally in problems with regular polygons, representing them in the complex plane and using the roots of unity as their vertices can simplify the geometry significantly.

Top