\ie\cf
\newcommand{\eqdef}{\mathbin{\stackrel{\rm def}{=}}}  \newcommand{\R} % real numbers  \newcommand{\N}} % natural numbers  \newcommand{\Z} % integers  \newcommand{\F} % a field  \newcommand{\Q} % the rationals  \newcommand{\C}{\mathbb{C}} % the complexes  \newcommand{\poly}}  \newcommand{\polylog}}  \newcommand{\loglog}}}  \newcommand{\zo}{\{0,1\}}  \newcommand{\suchthat}  \newcommand{\pr}[1]{\Pr\left[#1\right]}  \newcommand{\deffont}{\em}  \newcommand{\getsr}{\mathbin{\stackrel{\mbox{\tiny R}}{\gets}}}  \newcommand{\Exp}{\mathop{\mathrm E}\displaylimits} % expectation  \newcommand{\Var}{\mathop{\mathrm Var}\displaylimits} % variance  \newcommand{\xor}{\oplus}  \newcommand{\GF}{\mathrm{GF}}  \newcommand{\eps}{\varepsilon}  \notag
\no
Back to MB3

Week 15 Notes

100%

Congratulations on reaching the end of the course! Hopefully you've learned a lot during these \(15\) weeks. Now, it's time for you to apply your newfound knowledge.

Resources

Here are some great resources to continue your math journey.

Programs

There are a lot of great programs you can enroll in to continue participating in mathematics.

Learning

The internet is a deluge of information, and it's often hard to know where the best place to learn is. These are the sources I used most when needing to learn a subject.

Computing

Need to use some computer assistance to solve problems? The internet is brimming with online tools that can help.

Challenge: The Final Test

Here is a collection of \(14\) very challenging problems, each from each week of the course, to test how well you got the material. These problems should take you a decent amount of time, but solving them shows mastery over the material.

Given \(a+b+c=100\) with integers \(a,b,c\) satisfying \(0\lt a\lt b\lt c\), how many solutions are there to the equation?


Let \(w=a-1\), \(x=b-1-a\), \(y=c-1-b\), \(z=97-c\). Thus, \(w+x+y+z=94\), and \(w,x,y,z\) are all natural numbers. The number of ways of picking \(w,x,y,z\), which is equivalent to the answer we are looking for, can be computing via stars and bars to be \(97\choose3\).

On a train station, there are two intersecting lines: local trains and express trains. Local trains come every \(5\) minutes, starting at noon. Express trains come every \(6\) minutes, also starting at noon. John shows up to the train station at some random point during the day. What is the expected value of the amount of time he'll wait before a train shows up?


Every \(30\) minutes, both local and express trains come at the same time. So, let's draw a \(30\) minute timeline and the times at which trains show up.

We consider the expected value of the amount of time John waits if he shows up between each pair of consecutive trains. If John shows up between \(0\) and \(5\) minutes with probability \(\frac5{30}\), the expected wait time is \(\frac{0+5}2=2.5\) minutes. We can do a similar calculation for each of the time gaps in the diagram above, which is written underneath the timeline. So, the expected value is $$\frac1{30}(5\cdot2.5+1\cdot0.5+4\cdot2+\ldots+5\cdot2.5)$$Simplified, that becomes \(\frac{11}6\) minutes.

Consider all \(1000\) element subsets of \(\{1,2,\ldots,2022\}\). From each, choose the least element. What is the mean of all of the least elements?


There are \(2022\choose1000\) total \(1000\) element subsets. And, there are \(2022-k\choose999\) subsets of \(1000\) elements with least element \(k\) (since all of the remaining elements must be picked from the set \(\{k+1,\ldots,2022\}\)). Thus, our mean is $$\frac{1\cdot{2021\choose999}+2\cdot{2020\choose999}+\ldots+1023\cdot{999\choose999}}{2022\choose1000}$$Applying the Hockey Stick Identity \(1023\) times to the numerator, we get $$\frac{{2023\choose1000}+{2022\choose1000}+\ldots+{1000\choose1000}}{2022\choose1000}$$Applying the Hockey Stick Identity again, we have $$\frac{2023\choose1001}{2022\choose1000}=\frac{2023}{1001}=\frac{289}{143}$$

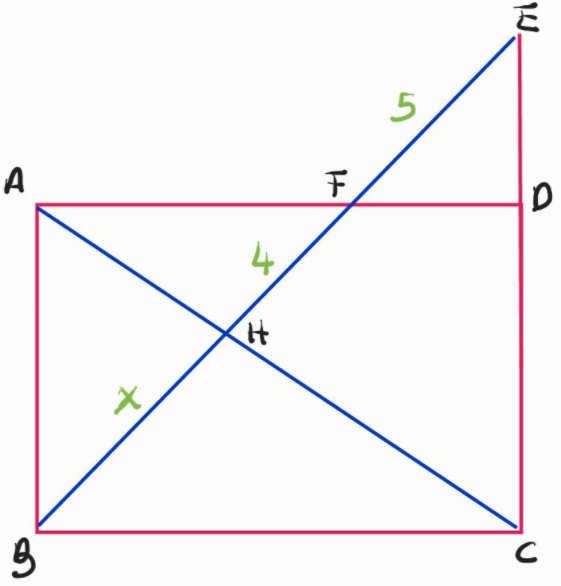
Given the following diagram, in which lines \(\overline{EB}\) and \(\overline{AC}\) intersect at point \(H\), and \(ABCD\) is a rectangle, find \(x\)


Since \(\angle FED=\angle ABF\) since \(\overline{AB}\) is parallel to \(\overline{CD}\), \(\triangle FED\sim\triangle EBC\). Let \(b=\overline{BC}\) and \(f=\overline{FD}\). By similarity, we have $$\frac fb=\frac5{9+x}\to 9f+fx=5b$$Since \(\angle DAC=\angle ACB\) as \(\overline{AD}\) and \(\overline{BC}\) are parallel, we have \(\triangle AFH\sim\triangle HBC\). By similarity, $$\frac{b-f}4=\frac bx\to bx-fx=4b$$Substituting \(f=\frac{bx-4b}x\) into the first equation gives us $$5b=9b\cdot\frac{x-4}x+bx-4b$$Dividing by \(\frac bx\) gives us $$\begin{aligned}5x&=9(x-4)+x^2-4x\\0&=x^2-36\\6&=x\end{aligned}$$

\(\;a_n\) and \(b_n\) are arithmetic sequences. Let \(S_n=\sum\limits_{i=1}^na_n\) and \(T_n=\sum\limits_{i=1}^nb_n\). If \(\frac{S_n}{T_n}=\frac{3n+1}{5n+3}\), what is \(\frac{a_5}{b_5}\)?


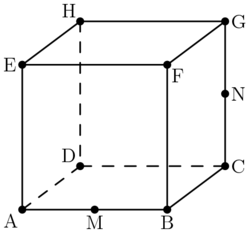
Since \(a_5\) is the average of the terms \(a_1,\ldots,a_9\) and similarly for \(b_5\), $$\frac{3\cdot9+1}{5\cdot9+3}=\frac{S_9}{T_9}=\frac{9a_5}{9b_5}=\frac{a_5}{b_5}$$Thus, the answer is \(\frac7{12}\).

In the unit cube below, \(M\) is the midpoint of \(\overline{AB}\) and \(N\) the midpoint of \(\overline{GC}\). The plane going through points \(D,B,C\) cuts the cube into two shapes. What is the volume of the smaller piece?

Hint: \(\triangle NDC\sim\triangle MBP\), where \(P\) is the intersection of the plane and \(\overline{BF}\).


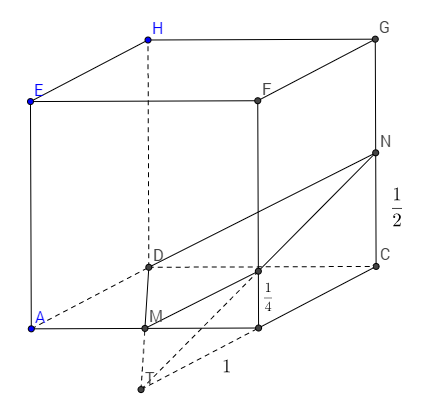
The trick is to realize that the smaller shape is just a pyramid (more precisely, a tetrahedron) with its top cut off, as in the following diagram.

As hinted, \(\triangle NDC\sim\triangle MBP\) since \(P\) is determined by the plane through \(D,M,N\). So, since \(MB=\frac12\) and \(DC=1\), \(\frac{NC}{PB}=\frac12\), so \(PB=\frac14\). That means that \(B\) is the midpoint of \(TC\), implying that \(TB=1\).


Finally, the area of \(\triangle NDC\) is \(\frac14\), so the volume of the whole pyramid \(TNDC\) is \(\frac14\cdot2\cdot\frac13=\frac16\). The area of the smaller pyramid \(TMBP\) is \(\frac1{16}\cdot1\cdot\frac13=\frac1{48}\), since the ratio of areas of similar triangles is the square of the ratio of the sides. So, our answer is \(\frac16-\frac1{48}=\frac7{48}\).

In the following diagram, \(a,b\) are positive real numbers. What is the value of \(\frac{\angle CDB}{\angle ADC}\)?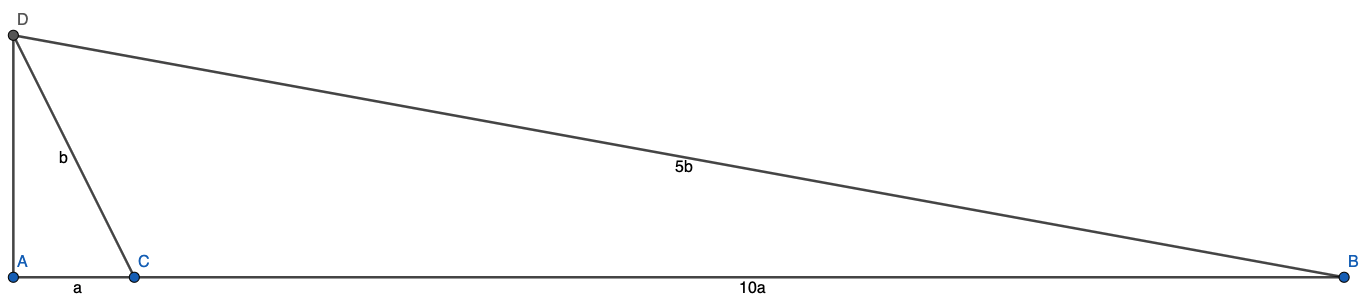


Let \(x=\overline{AD}\). By Pythagorean Theorem applied to both right triangles, we have $$x^2=b^2-a^2=25b^2-121a^2$$$$5a^2=b^2$$So, \(x=2a\).

Now, observe that the area of \(\triangle CDB\) is \(\frac12\cdot10a\cdot2a=10a^2\) since \(x\) is the height of the triangle. But, we can also use the formula \(A=\frac12ab\sin c\) to find the area, giving us $$\frac12b\cdot5b\cdot\sin\angle CDB=10a^2$$$$25a^2\sin\angle CDB=20a^2\to\sin\angle CDB=\frac45$$\(\sin\angle ADC=\frac1{\sqrt5}\) and \(\cos\angle ADC=\frac2{\sqrt5}\). Thus, $$\sin\angle ADC\cdot\cos\angle ADC=\frac25=\frac12\sin\angle CDB$$By our double angle formula, \(\sin2\theta=2\sin\theta\cos\theta\), so \(\angle CDB=2\angle ADC\).

What is the smallest natural number \(n\) such that $$2^0+2^1+\ldots+2^n\equiv0\bmod{77}$$


\(2^{n+1}\equiv1\bmod{77}\) since the sum equals \(2^{n+1}-1\). Thus, by the Chinese Remainder Theorem, we need to find \(n\) such that \(2^{n+1}\equiv1\bmod7\) and \(2^{n+1}\equiv1\bmod{11}\). By the Totient Theorem, \(2^6\equiv1\bmod7\) and \(2^{10}\equiv1\bmod{11}\).

So, we check the divisors of \(6\) and \(10\) to see if there is a smaller power that works as well. We find \(2^3\equiv1\bmod7\), and no divisor of \(10\) works mod \(11\). So, the smallest \(n+1\) that works is \(3\cdot10=30\). Thus, our answer is \(29\).

Compute $$\sum\limits_{n=1}^\infty\frac1{n^2+4n+3}$$


Factoring the denominator gives us $$\sum\limits_{n=1}^\infty\frac1{(n+1)(n+3)}$$Decomposing this fraction into two gives us $$\frac12\left(\frac1{n+1}-\frac1{n+3}\right)=\frac1{n^2+4n+3}$$So, our sum becomes $$\frac12\sum\limits_{n=1}^\infty\frac1{n+1}-\frac1{n+3}$$The first few terms of the sum are \(\frac12-\frac14\), \(\frac13-\frac15\), \(\frac14-\frac16\), etc. All of the terms except \(\frac12\) and \(\frac13\) cancel. So the sum becomes $$\frac12\cdot\left(\frac12+\frac13\right)=\frac5{12}$$

Write in second order logic the axioms of the real numbers (assume that there are binary operations \(+\) and \(\cdot\) and an order operation \(\lt\) defined). Hint: All but one of the axioms can be written in first order logic.


This is a bit of an unfair question, as we haven't really learned about the real numbers, but it's meant as an exercise to test your understanding of number systems you work with. \(\veebar\) represents XOR, the operation that is true iff exactly one of the inputs is true. Here are the axioms and their names (The last one is a second order axiom):
NameAxiom
Additive Associativity\(\forall a,b,c,\;a+(b+c)=(a+b)+c\)
Additive Identity\(\exists0\forall a,\;a+0=a\)
Additive Inverse\(\forall a\exists b,\;a+b=0\)
Additive Commutativity\(\forall a,b,\;a+b=b+a\)
Multiplicative Associativity\(\forall a,b,c,\;a\cdot(b\cdot c)=(a\cdot b)\cdot c\)
Multiplicative Identity\(\exists 1\neq0\forall a,\;1\cdot a=a\)
Multiplicative Inverse\(\forall a\neq0\exists b,\;a\cdot b=1\)
Multiplicative Commutativity\(\forall a,b,\;a\cdot b=b\cdot a\)
Distributivity\(\forall a,b,c,\;a\cdot(b+c)=a\cdot b+a\cdot c\)
Trichotomy\(\forall a,\;(a\lt0)\veebar(a=0)\veebar(a\gt0)\)
Additive Closure\(\forall a,b,\;a\gt0\wedge b\gt0\to a+b\gt0\)
Multiplicative Closure\(\forall a,b,\;a\gt0\wedge b\gt0\to a\cdot b\gt0\)
Least Upper Bound$$\begin{aligned}\forall\text{ properties }P,\;(\exists u\forall a,\;Pa\to a\lt u)\\\to\exists l,\;(\forall a,\;Pa\to a\lt l)\wedge\forall u(\forall a,\;Pa\to a\lt u),\;l\leq u\end{aligned}$$

Given the polynomial \(x^3+ax^2+bx+c\), if \(p,q,r\) are the roots of the polynomial, what is the value of \(p^4+q^4+r^4\)?


By Vieta's, we know that \(pqr=-c\), \(pq+qr+rp=b\), and \(p+q+r=-a\). First, let's find \(p^2+q^2+r^2\). $$\begin{aligned}a^2=p^2+q^2+r^2+2(pq+qr+rp)\\p^2+q^2+r^2=a^2-2b\end{aligned}$$Now, we find \(p^3+q^3+r^3\)$$\begin{aligned}-a^3=-2(p^3+q^3+r^3)+6pqr+3pqr(p^2+q^2+r^2)\\p^3+q^3+r^3=\frac{a^3-3c(a^2-2b+2)}2\end{aligned}$$Next, we find \(p^2q^2+q^2r^2+p^2r^2\)$$\begin{aligned}b^2=p^2q^2+q^2r^2+p^2r^2+2pqr(p+q+r)\\p^2q^2+q^2r^2+r^2p^2=b^2-2ac\end{aligned}$$So, $$\begin{aligned}a^4=-3(p^4+q^4+r^4)+4pqr(p^3+q^3+r^3)+6(b^2-2ac)+12pqr(p+q+r)\\p^4+q^4+r^4=\frac13\left(6c^2(a^2-2b+2)-2a^3c+6b^2\right)\end{aligned}$$

Given a sequence \(A_n\) with \(A_1=1\) and $$A_{n+1}=\frac{A_n}{1+nA_n}$$Compute \(A_{2022}\)


Let's manipulate the recursion to a form easier to handle. Inverting both sides gives us $$\frac1{A_{n+1}}=\frac{1+nA_n}{A_n}=n+\frac1{A_n}$$Letting \(B_n=\frac1{A_n}\), we have \(B_1=1\) and \(B_{n+1}=n+B_n\). Thus, \(B_n=1+\frac{n(n+1)}2=\frac{n^2+n+2}2\). So, $$A_n=\frac2{n^2+n+2}$$So, \(A_{2022}=\frac1{2\cdot1011^2+1012}\).

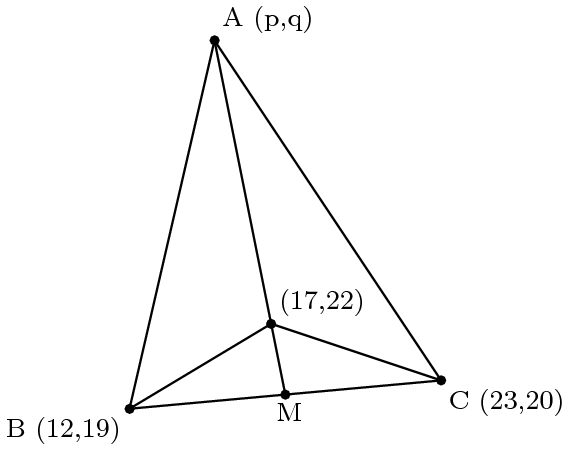
\(\;\triangle ABC\) in the following diagram has area \(70\). The median \(\overline{AM}\) has slope \(-5\). Find the maximum value of \(p+q\).


We could simply bash this out using coordinate geometry, but a faster solution uses the Shoelace Theorem. The area of the triangle via the Shoelace Theorem is \(\frac12|-p-197+11q|\), so $$|p+197-11q|=140$$Via the point-slope form of a line, we can find the equation of \(\overline{AM}\) to be \(y=-5x+107\). Plugging in point \(A\) into this equation gives us \(q\) in terms of \(p\). Plugging that into the Shoelace formula gives us $$|980-56p|=140\to980-56p=\pm140$$Solving these two possibilities gives us \(p=15,20\), which correspond to \(q=32,7\). Thus, the answer is \(15+32=47\).

Find the positive real value \(x\) that satisfies $$x^{x^x}=\left(\frac12\right)^{\sqrt2}$$


Log both sides to get \(x^x\log_2x=-\sqrt2\) since \(\log_2\frac12=-1\). Divide both sides by \(\log_2x\) and log both sides again to get $$x\log_2x=\log_2\left(\sqrt2\cdot\frac{-1}{\log_2x}\right)=\frac12-\log_2(-\log_2x)$$This implies that \(x\lt1\) since \(\log_2x\lt0\) (otherwise the rightmost log wouldn't be defined.) Additionally, since every term we've seen is a power of \(2\), it's a fair guess to try letting \(x=2^{-k}\) for some natural \(k\). With this, we get $$k2^{-k}+2^{-1}=\log_2(k)$$Raising both sides with a base of \(2\) gives us $$k=2^{0.5+k2^{-k}}$$For \(k\) to be a natural number, \(0.5+k2^{-k}\) must be an integer. Clearly, this is only possible if \(k=2\). Plugging in \(2^{-2}=\frac14\) into the original equation, we see that it is a solution, and we are done.
Top