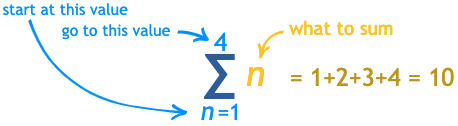\ie\cf
\newcommand{\eqdef}{\mathbin{\stackrel{\rm def}{=}}}  \newcommand{\R} % real numbers  \newcommand{\N}} % natural numbers  \newcommand{\Z} % integers  \newcommand{\F} % a field  \newcommand{\Q} % the rationals  \newcommand{\C}{\mathbb{C}} % the complexes  \newcommand{\poly}}  \newcommand{\polylog}}  \newcommand{\loglog}}}  \newcommand{\zo}{\{0,1\}}  \newcommand{\suchthat}  \newcommand{\pr}[1]{\Pr\left[#1\right]}  \newcommand{\deffont}{\em}  \newcommand{\getsr}{\mathbin{\stackrel{\mbox{\tiny R}}{\gets}}}  \newcommand{\Exp}{\mathop{\mathrm E}\displaylimits} % expectation  \newcommand{\Var}{\mathop{\mathrm Var}\displaylimits} % variance  \newcommand{\xor}{\oplus}  \newcommand{\GF}{\mathrm{GF}}  \newcommand{\eps}{\varepsilon}  \notag
\no
Back to MB3

Week 2 Notes

100%

Before we start this week's notes, I want to introduce some notation you may not have seen before.

Let's say I want to add all of the numbers from \(1\) to \(n\). I would write it like this: $$1+2+\ldots+n$$In mathematics, we don't like using \(\ldots\) since it can be unclear. Instead, we have a notation to represent this sort of sum. $$\sum\limits_{k=1}^nk=1+2+\ldots+n$$This diagram explains what the \(\Sigma\) notation means:

We can even do fancier things with \(\Sigma\). We can sum squared numbers:$$\sum\limits_{k=1}^4k^2=1^2+2^2+3^2+4^2=30$$We can add the first \(6\) odd numbers:$$\sum\limits_{k=1}^62k-1=36$$There are many things we can do with this notation. If you are still a bit confused, try using the Sigma Calculator to play around with \(\Sigma\). Here is a challenging exercise that really tests your understanding of the notation.

Evaluate $$\sum\limits_{n_{2021}=0}^2\sum\limits_{n_{2020}=0}^{n_{2021}}\sum\limits_{n_{2019}=0}^{n_{2020}}\ldots\sum\limits_{n_1=0}^{n_2}1$$


Note that $$2\geq n_{2021}\geq n_{2020}\geq\ldots\geq n_1\geq0$$Since the innermost summand is \(1\), this nested summation is just ocunting how many choices of variables \(n_{2021},\ldots,n_1\) satisfy the above property. We can apply stars and bars to solve this problem.

Let there be \(2021\) stars, representing our \(2021\) variables. Let there be \(2\) bars. Given any sequence of these \(2023\) objects, we can set \(n_k\) for \(1\leq k\leq 2021\) to be the number of bars after the \(k\)th star in the sequence. I'll leave it to you to verify that this satisfies all of our conditions. So, the answer is just the number of ways to place \(2\) bars in the sequence of \(2023\) objects, which is just $${2023\choose 2}=\frac{2023\cdot2022}2=\color{red}{2045253}$$

What is Probability?

This week's topic will be all about probability. Probability is one of the hardest subjects you'll encounter in competitions, not least because of how counterintuitive it can be. But what even is probability?

We say that an event is an activity or process that involves chance. Probability, therefore, is the likelihood of an event having some outcome.

For example, one event might be throwing a die. An outcome might be rolling an even number. The probability of this outcome is \(\frac36=\frac12\).

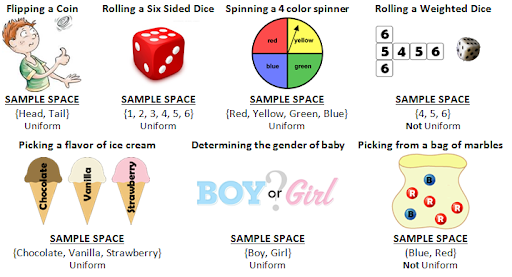
We call the set of all possible outcomes the sample space of our event. Here are some examples of sample spaces:

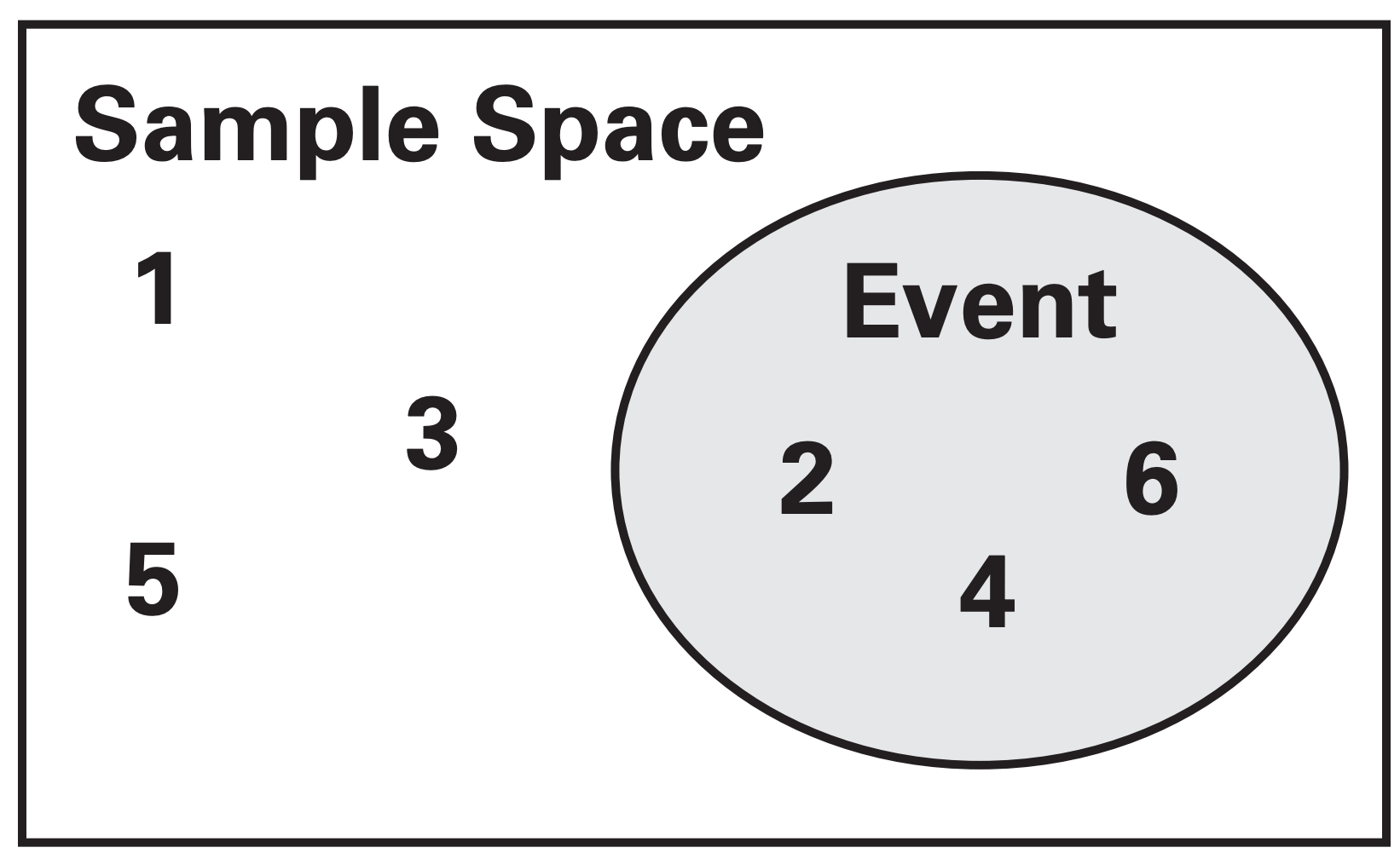
For events with small sample spaces, we can draw a Venn Diagram to represent our problem. For example, if we take our die example from earlier:

Our sample space is the set \(\{1,2,3,4,5,6\}\) while our favorable outcome space is \(\{2,4,6\}\). Using these diagrams may seem silly, but they are actually quite helpful!

Now how do we find the probability of our event having a favorable outcome? This is a tough question. However, it is not so tough when our sample space is uniform, meaning that every outcome in the sample space is equally likely! In this case, the probability of a favorable outcome occuring is: $$P(\text{favorable outcome})=\frac{\text{Number of favorable outcomes}}{\text{Total number of outcomes in sample space}}$$

Suppose I draw a random card from the top of a standard \(52\) card deck. What is the probability that
  • The card drawn is a King
  • The card drawn is a club


  • There are \(52\) cards in our sample space. \(4\) cards are Kings. So, the answer is $$P(\text{King})=\frac4{52}=\frac1{13}$$
  • There are \(52\) cards in our sample space. \(13\) cards are clubs. So, the answer is $$P(\text{Club})=\frac{13}{52}=\frac14$$

As you see in the exercise above, when the sample space is uniform (all possibilities are equally likely), finding the probability is about counting the number of favorable outcomes. That also means that permutations and combinations are important in calculating probability.

Your class has \(12\) girls and \(11\) boys. Your teacher selects \(4\) students uniformly to present their projects.
  • What is the probability all \(4\) students are girls?
  • Suppose the teacher chose Andy, Ciara, Beth, and Eugene. The teacher also chose which order they'd present randomly. What is the probability that they will present in alphabetical order?


  • There are \(_{23}C_4\) ways to choose \(4\) students from the class. There are \(_{12}C_4\) ways of choosing \(4\) girls from the class. So, our answer is $$\frac{_{12}C_4}{_{23}C_4}=\frac{495}{8855}=\frac5{161}$$
  • There are \(_4P_4=4!\) ways to choose an ordering of \(4\) students to present. There is \(1\) way for that ordering to be alphabetical. So, our answer is $$\frac1{4!}=\frac1{24}$$

Law of Large Numbers

In the summer of 1913 in the Casino de Monte-Carlo, hundreds of people were playing Roulette, a game in which one bets on whether the rotating ball will fall on a red or black spot. On average, it will land on a red spot \(50\%\) of the time. However, on this special day, the ball landed on a black spot \(26\) times in a row.

This made newspaper headlines! One newspaper asked readers, if the roulette was spun again, which spot was the ball most likely to fall in? There were some competing theories:

So which of these arguments is right? Neither! As surprising as \(26\) rolls in the black is to us, it doesn't indicate that something is wrong with the machine. After all, every sequence of \(26\) rolls is equally likely. It also doesn't mean that the next roll will also be black. Here's a funny comic showing why this argument doesn't work.

As for the second argument, every roll is independent, meaning that each roll doesn't depend on what happened before it. It doesn't matter how many black rolls there were before, the probability of a red roll now is still \(50\%\). The universe doesn't "correct" for the past results.

This second argument is sometimes called the "Law of small numbers" (in quotations since it is false), as it suggests that the universe will always try to balance out the number of reds and blacks rolled. Here's a comic that illustrates why this logic is wrong, too.

So if the "Law of small numbers" is false, then what is true? The Law of Large Numbers says that on average, if event \(X\) has probability \(p\) of occuring, the more times I do the experiment, the fraction \(\frac{\text{number of success}}{\text{number of experiments}}\) will be closer to \(p\).

Note: This is a very, very tricky concept. If this is new to you, I'd suggest re-reading this section, or reading about this topic somewhere else to become more familiar with the ideas here. I'll try to talk about this in class as well.

Independent Events

In the last section, we said that the rolls of the roulette are independent. What does this mean?

Given events \(A\), \(B\) in the same sample space, \(A\) and \(B\) are independent iff $$P(A\text{ and }B)=P(A)\cdot P(B)$$

Let's look at some examples to understand this definition.

For each of the following pairs of events, determine whether the events are dependent or independent:
  • I have a drawer with \(10\) white socks and \(10\) black socks. I select two socks from my drawer randomly. \(A\) is the event that my first sock is white. \(B\) is the event that both socks selected are of the same color.
  • I select a random letter from the alphabet. \(A\) is the event that it is a vowel (a,e,i,o,u). \(B\) is the event that it is a consonant (any letter that isn't a vowel).
  • You roll a die two times. \(A\) is the probability you get a \(5\) on your first roll. \(B\) is the probability you get an even number on your second roll.

As you saw from the examples and exercises above, not all events are independent. Dependent events tell you something about each other. For example, if I know that tomorrow, the temperature outside will be \(80^\circ\), I know that the probability of a snowstorm will be very low. We call this conditional probability.

Given events \(A,B\), we define \(P(A\mid B)\), the probability of \(A\) given that we know \(B\) happens, as $$P(A\mid B)=\frac{P(A\text{ and }B)}{P(B)}$$

In other words, when \(A,B\) are independent, \(P(A\mid B)=P(A)\). This makes sense, because \(B\) tells us nothing about \(A\).

Compute the following probabilities:
  • \(P(B)=0.7,\;P(A\mid B)=0.3\), compute \(P(A\text{ and }B)\)
  • \(P(A)=0.9,\;P(B|A)=0.72\), compute \(P(A\text{ and }B)\)
  • \(P(A\text{ and }B)=0.15,\;P(B\mid A)=0.6\), compute \(P(A)\)

Mutually Exclusive Events

Sometimes, there are events that are mutually exclusive, meaning they can't both happen. For example, a coin flip can't be both heads and tails.

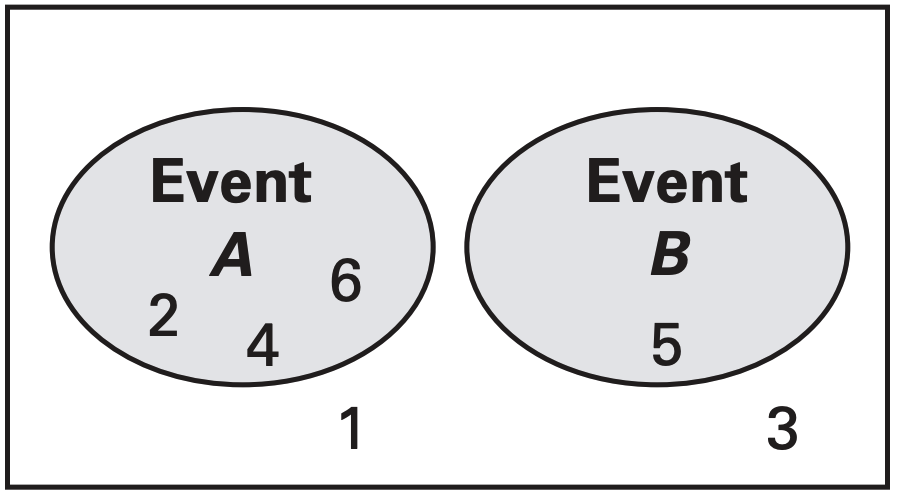
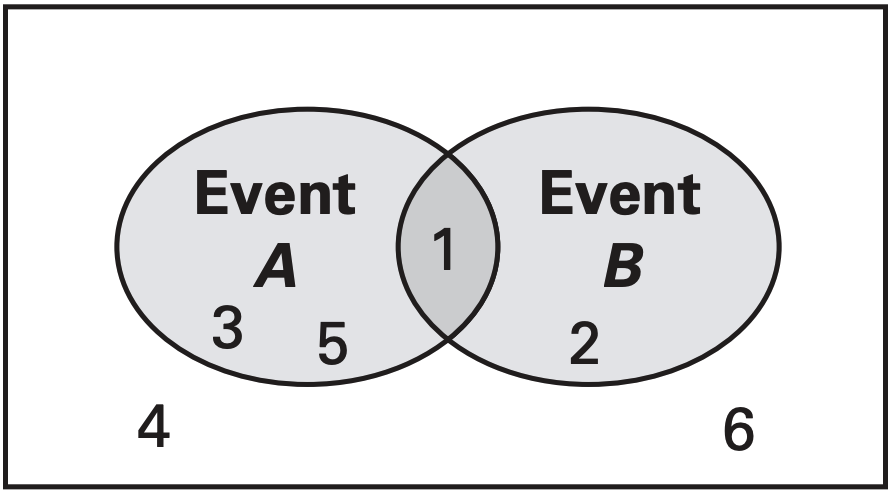
Given events \(A,B\), they are mutually exclusive iff \(P(A\text{ and }B)=0\).

We call events that are not mutually exclusive overlapping. Below are examples of mutually exclusive and overlapping events.

Let's take a closer look at the overlapping events. Our sample space is rolling a die. Event \(A\) is rolling an odd number, and event \(B\) is rolling a number \(\lt3\). What is the probability of at least one of \(A\) and \(B\) happening? We can see by inspection that it is \(\frac46\). But, \(P(A)+P(B)=\frac36+\frac26=\frac56\).

What is going on here? The issue is, we are double counting the event of rolling \(1\). In general, we overcount the cases that both \(A\) and \(B\) occur. That gives us the very important formula $$P(A\text{ or }B)=P(A)+P(B)-P(A\text{ and }B)$$For mutually exclusive events, this becomes $$P(A\text{ or }B)=P(A)+P(B)$$

I have a bag with the following marbles:
Type Number
Blue 12
Green 9
Red 5
Yellow 4
I pick a random marble from the bag. What is the probability of the chosen marble being either red or yellow?

Since these events are mutually exclusive, we have $$P(\text{red or yellow})=P(\text{red})+P(\text{yellow})=\frac4{30}+\frac5{30}=0.3$$
In each scenario, explain why the events are mutually exclusive or overlapping:
  • You conduct a survey of pet ownership. Event \(A\): the respondent is a cat owner. Event \(B\): the respondent is a dog owner.
  • Event \(A\): Your best friend plays the clarinet. Event \(B\): Your friend hates playing musical instruments.

Continuous Probability

In all of our examples so far, our state spaces have been finite (for example, the \(6\) outcomes of the roll of a die.) Let's consider the following question: Suppose I pick a point in the unit circle. What is the probability that is at most \(0.5\) away from the center of the circle?

To answer this, let's remember our formula for probability: $$P(\text{favorable outcome})=\frac{\text{Number of favorable outcomes}}{\text{Total number of outcomes in sample space}}$$The issue with this formula is that there are infintely many points in our circle. So, the fraction would become \(\frac\infty\infty\), which is silly!

Instead, if we replace Number with Area, we get a formula we can work with: $$P(\text{favorable outcome})=\frac{\text{Area of region of favorable outcomes}}{\text{Area of sample space}}$$Using this new formula, we see that the region of points that are at most \(0.5\) away from the center is just the circle of radius \(0.5\) around the center, which has area \(\frac\pi4\). The unit circle has area \(\pi\), so our answer is $$\frac{\frac\pi4}\pi=\frac14$$

Let \(x,y\) be randomly chosen real numbers between \(0,1\). What is the probability that \(y-x>0.5\)?

Challenge: Expected Value

In the notes so far, we've discussed probability rather informally. Let's be a bit more precise.

A random variable is just a quantity that varies randomly. For example, \(D_6\) is the random variable that represents the roll of one die. It takes values \(\{1,2,3,4,5,6\}\), each with probability \(\frac16\).

Given a random variable, we might want to ask, what is the average value of the random variable? Well, that is simple to calculate. It is just $$E[R]=\sum\limits_{x\in S}x\cdot P(x)$$The idea behind this summation is as follows. We are taking a sum over all \(x\) in the state space \(S\), and for each \(x\), we are adding the term \(x\cdot P(x)\).

As an example, $$E[D_6]=1\cdot\frac16+2\cdot\frac16+\ldots+6\cdot\frac16=3.5$$Expected value is a very useful concept because it is a linear function. If I have random variables \(X_1,\ldots,X_n\), then $$E[X_1+X_2+\ldots+X_n]=E[X_1]+E[X_2]+\ldots+E[X_n]$$Here are some exercises to test your understanding.

There are \(n\) people in a room, and \(n\) name tags, each for one person. However, the name tags are handed out randomly so that each person gets one random tag. What is the expected value of the number of people who get their own tag?


\(1\)
\(\;2020\) babies sit in a circle, and each one either pokes the baby to its right, or to its left, with equal probability. What is the expected number of unpoked babies?


\(505\)
There are \(13\) girls and \(7\) boys in the class. They are randomly put into a line. What is the expected number of places where a girl and a boy are standing next to each other?


\(9.1\)
Top