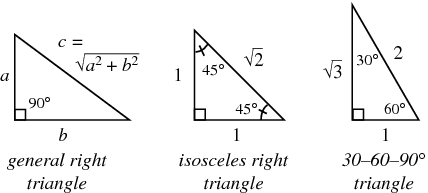Week 4 Notes
- Similar Triangles
- Cevians
- Area of a Triangle
- Isosceles Triangles
- Right Triangles
- Equilateral Triangles
- Other properties of Triangles
- Challenge: Mass Points
This week's notes are all about triangles! Unfortunately, there are a lot of formulas in these notes. I don't want you to be memorizing most of them, but hopefully they give you an idea as to what is possible with triangles. Once we learn some trigonometry in a few weeks, we can understand these formulas a bit better.
Similar Triangles
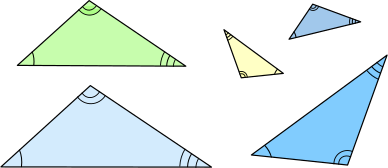
Two triangles are similar if the only difference between them is their size (and possible the need to turn/flip around). The triangles below are all similar
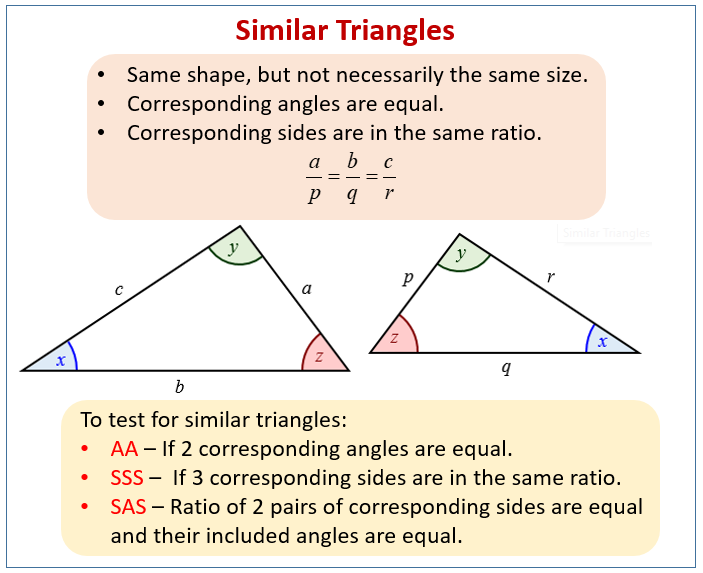
Similar triangles are very useful since all similar triangles have equal corresponding angles
And the ratio of their corresponding sides is the same for all sides
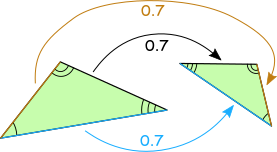
Congruent triangles are similar triangles for which the ratio of corresponding sides is \(1\). How can we tell if two triangles are similar?
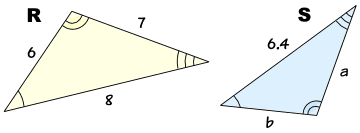
- AA: If two of the angles of one triangle equal two of the angles of the other triangle, they are similar
- SAS: If the ratios of two sides of one triangle with two sides of the other triangle are the same, and the angles between these two sides in the first triangle is the same as the corresponding angle in the other triangle, the triangles are similar.
- SSS: If the ratios of all three sides with their corresponding sides is the same, the triangles are similar
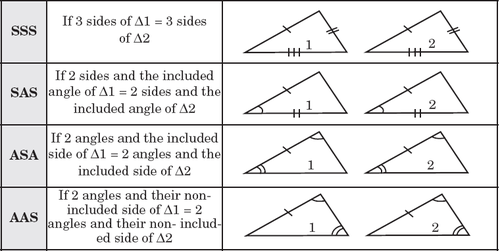
This diagram summarizes the statements above.
To tell whether two triangles are congruent, we have similar conditions
- AAS: If any two angles from the first triangle equal any two angles from the second triangle, and a side from the first triangle equals a corresponding side in the other triangle, the triangles are congruent.
- SAS: If two sides from the first triangle are equal to two sides of the other triangle, and the angle between the sides is equal to the same angle in the other triangle, the triangles are congruent.
- SSS: If all three sides are equal to the three sides of the other triangle, the triangles are congruent.
The following diagram summarizes the statements above.
Important: Given similar triangles \(A,B\) such that the ratio of sides is \(x\), the ratio of their perimeters is \(x\) and the ratio of their areas is \(x^2\).
Cevians
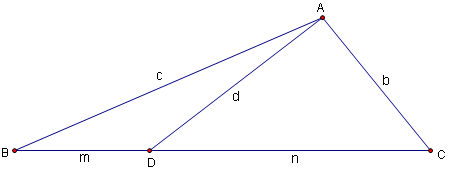
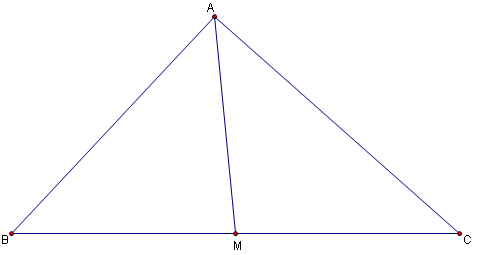
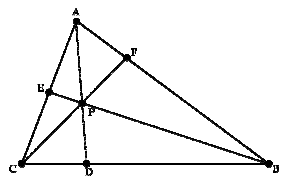
Many triangle problems you will encounter will deal with cevians. A cevian is a line segment starting at a vertex of a triangle, and ending at the opposite side. In the diagram below, \(\overline{AD}\) is a cevian of \(\triangle ABC\) with side lengths \(a,b,c\).
One of the most famous cevian formulas has the following mnemonic: "A man and his dad put a bomb in the sink."$$man+dad=bmb+cnc$$This formula, known as Stewart's Theorem, works with all cevians. However, there are three special types of cevians you should know how to work with.
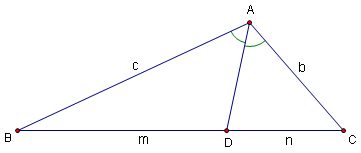
Angle Bisector
An angle bisector is a cevian that splits the angle in half. In the diagram above, we see that \(\angle BAD=\angle CAD\), meaning that the cevian is an angle bisector.
This exercise implies that \(bm=cn\). In fact, if \(bm=cn\) for any cevian, the cevian is an angle bisector.
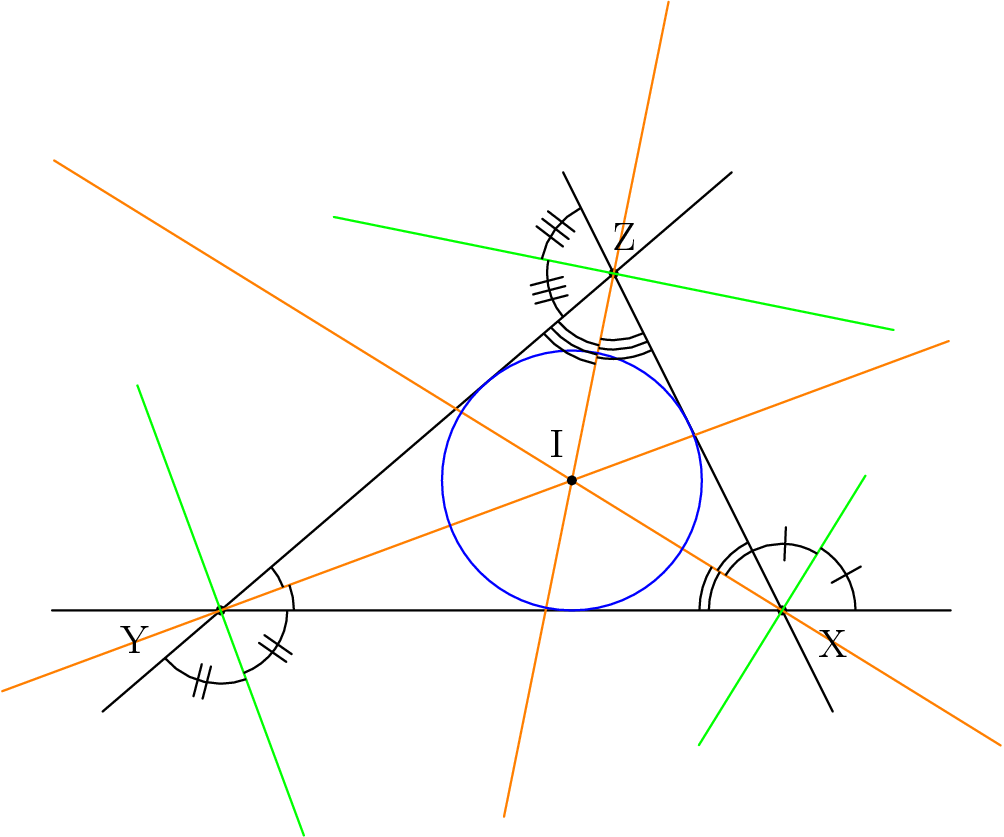
Surprisingly, all \(3\) angle bisectors of a triangle intersect at a single point, which is called the incenter because it is the center of the inscribed circle of the triangle (see the next diagram).
Median
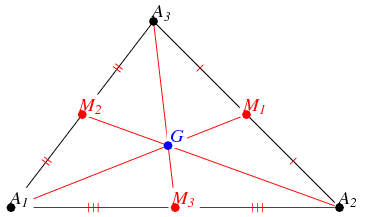
The median is a cevian which intersects the midpoint of the opposing side to the vertex. In the cevian diagram above, the cevian is a median iff \(m=n\).
Like the angle bisectors, the three medians also meet at a common point, called the centroid, as in the diagram below.
And, \(\overline{A_3G}=2\overline{GM_3}\). This relationship comes in handy in a lot of geometry problems.
Altitude
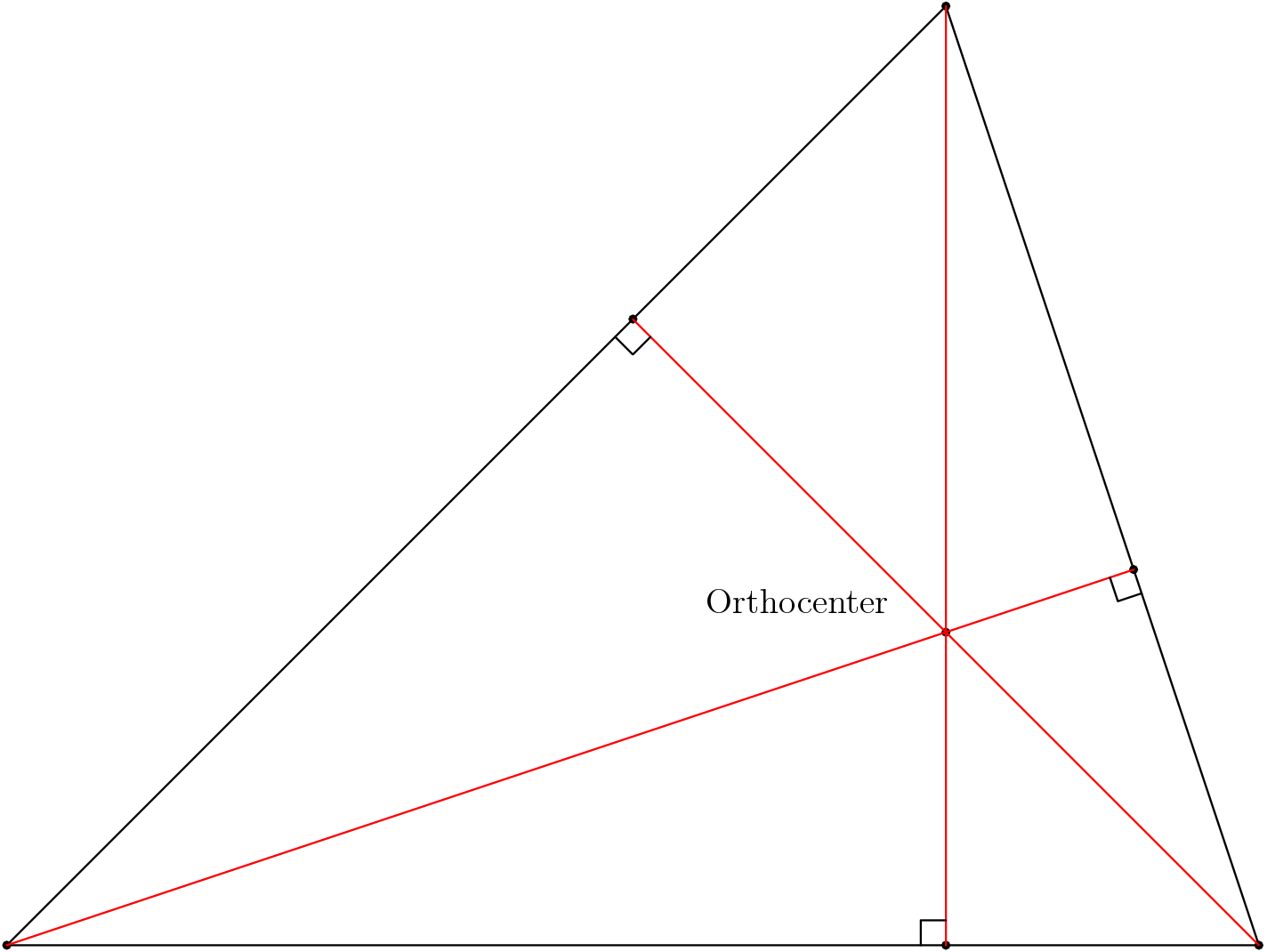
The altitude is a cevian which is perpendicular to the side of the triangle it intersects.
The most important thing to know about the altitude is the area formula (in the next section). However, altitudes also have special relationships with the circumcenter (center of the circumscribing circle) and incenter. Let \(R\) be the radius of the circumcircle and \(r\) the radius of the incircle.
Let \(O\) be the circumcenter of the triangle, and let \(D\) be the midpoint of side \(AB\). Then, \(AD=BD\), \(OD=OD\), and \(AO=BO\) since they are both radii. By \(SSS\), \(\triangle ADO\cong\triangle BDO\), which implies that \(\angle ADO=\angle BDO\). But, \(\angle ADO+\angle BDO=180^\circ\) as \(AB\) is a line, so \(\angle ADO=90^\circ\). Thus, \(OD\) is the perpendicular bisector of \(AB\), and thus, \(O\) is on the perpendicular bisector of \(AB\).
Like the other two special cevians, all altitudes intersect at one point, which we call the orthocenter. If the lengths of the altitudes are \(h_a,h_b,h_c\), then the following formulas are true:$$h_ah_bh_c=\frac{(abc)^2}{8R^3}$$$$\frac1{h_a}+\frac1{h_b}+\frac1{h_c}=\frac1r$$where \(R\) is the radius of the circumcircle and \(r\) the radius of the incircle.
Area of a Triangle
Here are some useful area formulas for triangles:
- Given a triangle with side length \(b\) (which we call the base) and altitude \(h\) to the base (which we call the height), the area of the triangle is \(\frac12bh\).
- Given a triangle with sides \(a,b,c\) and circumradius \(R\), the area of the triangle is $$\frac{abc}{4R}$$
- If you have a triangle with coordinates \((x_1,y_1)\), \((x_2,y_2)\), \((x_3,y_3)\), the area is given by $$\frac12\cdot\left\vert x_1y_2-x_2y_1+x_2y_3-x_3y_2+x_3y_1-x_1y_3\right\vert$$
- triangle with sides \(a,b,c\) and semiperimeter \(s=\frac{a+b+c}2\) has area $$\sqrt{s\cdot(s-a)(s-b)(s-c)}$$
- If \(m_1,m_2,m_3\) are the medians of the triangle, and \(s=\frac12(m_1+m_2+m_3)\), then the area is $$\sqrt{s\cdot(s-m_1)(s-m_2)(s-m_3)}$$
Isosceles Triangles
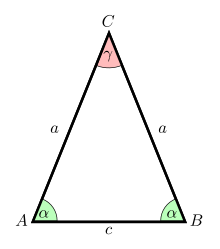
An isosceles triangle is a triangle with at least two sides equal.
One of the most important properties of an isosceles triangle is the Hinge property: the angles opposing the equal sides are also equal (which you can see in the diagram above).
Right Triangles
A right triangle is any triangle with a \(90^\circ\) angle. You should already know plenty about right triangles (after all, all of our work with Pythagorean triples is about right triangles!).
As seen in the diagram above, there are a few special right triangles you might want to remember. The first is the isosceles right triangle, with its hypotenuse with length \(\sqrt2\) times the length of both legs. The second is the \(30-60-90\) triangle, with side lengths \(x,\;\sqrt3x,\;2x\).
Since each leg of the triangle is a height to the other leg, the product of the lengths of the legs of a right triangle is twice the area of the triangle. Moreover, the circumcircle of a right triangle has diameter equal to the hypotenuse of the triangle.
Equilateral Triangles
An equilateral triangle is a triangle with all equal sides (or equivalently, all angles equal to \(60^\circ\)). By definition, all equilateral triangles are similar. Using the area of an isosceles formula and setting \(a=b\), we get the area of the equilateral triangle to be \(\frac{a^2\sqrt3}4\).
Other properties of triangles
There are other types of triangles (obtuse, which has an angle with more than \(90^\circ\) degrees, acute, whose angles are all less than \(90^\circ\), and scalene, which has \(3\) unequal sides) but these triangles don't have many special formulas. Here are some general results about triangles that are useful!
- The inradius (radius of the inscribed circle) of a triangle with side lengths \(a,b,c\) and area \(K\) is $$r=\frac{2K}{a+b+c}$$
- The sum of any two sides of a triangle is greater than the third side.
Challenge: Mass Points
Mass Points are a cute technique that allow us to solve cevian problems without having to do too much solving. To understand how they work, let's first understand torque.
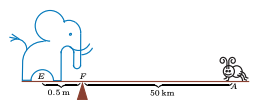
Suppose I have a see-saw, and I want to balance an elephant and an ant on the see-saw. Our elephant weighs \(100kg\) (it's a baby elephant) and our ant weighs \(1\) gram. So how do we balance the two?
A see-saw is balanced when the torque on both sides is \(0\). Torque is the distance from the balancing point (which we call the fulcrum) times the weight. So if the baby elephant is \(0.5m\) away from the fulcrum, then the ant must be \(\frac{100 kg\cdot0.5 m}{0.001kg}=50km\) away from the fulcrum for the see-saw to balance. That's a long see-saw!
Mass Points is all about applying this concept to geometry, by assigning weights to points in our diagram to balance around certain points.
To summarize, here are the properties of mass points
- See-saw: For any line segment \(AEC\) with a fulcrum at \(E\), and \(m(X)\) referring to the mass at point \(X\),$$m(A)\cdot\overline{AE}=m(C)\cdot\overline{CE}$$This is just our see-saw example with the elephant and ant generalized.
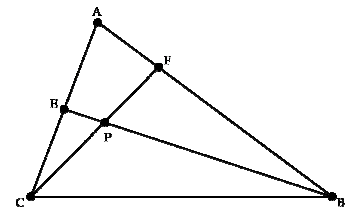
- $$m(E)=m(A)+m(C)$$To understand this rule, consider the diagram If we choose the weights at points \(A,B,C\) well, the diagram will balance at point \(P\). We can view this diagram as a see-saw \(BPE\), with \(E\) itself being a see-saw \(AEC\), as in the following diagram:Thus, we can replace the see-saw on the right with a weight whose value is the sum of the weights on the see-saw. This gives us the desired relation.
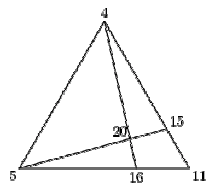
To test our understanding, let's solve some problems!
To test our understanding, let's solve some problems!
Now that you've gotten a feel for how mass point can be used to solve problems, here are some exercises.