Week 5 Notes
This week is Countdown week, so the notes are going to be a bit shorter than normal.
Take some time to review the material from the first 4 weeks.
Sequences
What is a sequence? Well, it is just an infinite list of numbers. That's it, really. There are two special types of sequences we care about, however.
Arithmetic Sequence
Geometric Sequence
Unlike arithmetic sequences, which we can only take finite sums of, we can consider infinite sums of geometric sequences. Suppose I have a geometric sequence \(a_1,\ldots\), with \(r=\frac{a_2}{a_1}\).
If \(|r|\geq1\), then it is clear that unless \(a_1=0\), \(\sum\limits_{i=1}^\infty a_i\) is \(\pm\infty\), or just not defined.
But, if \(|r|\lt1\), \(\sum\limits_{i=0}^\infty ar^i\) has a finite value. Here's how we can find it.
Let \(S=\sum\limits_{i=0}^\infty ar^i\). So, $$S=a+ar+\ldots$$$$rS=ar+ar^2+\ldots$$$$a+rS=a+ar+\ldots=S$$$$a+rS=S$$$$S=\frac a{1-r}$$
As an example of geometric series, suppose we wanted to compute the sum of all of the divisors of \(n\). We'd first prime factorize \(n\) as \(p_1^{e_1}p_2^{e_2}\ldots p_k^{e_k}\). Then, we observe that all divisors of \(n\) are of the form \(p_1^{a_1}\cdot\ldots\cdot p_k^{a_k}\), where \(a_i\leq e_i\) for each \(i\). Thus, the sum of divisors of \(n\) is $$(1+p_1+\ldots+p_1^{e_1})\cdot\ldots\cdot(1+p_k+\ldots+p_k^{e_k})$$However, each term is a geometric series, so we can replace each term by \(\frac{p_i^{e_i+1}-1}{p_i-1}\). Thus, our formula becomes $$\prod\limits_{i=1}^k\frac{p_k^{e_k+1}-1}{p_k-1}$$ (Side Note: \(\prod\) is similar to \(\sum\), except it is for products rather than sums.)
Challenge: Convexity
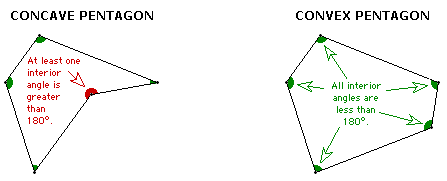
You may have learned about convex polygons before.
Why do we call these polygons convex? What does it mean to be convex? In this section, we'll only be concerned with shapes in the cartesian plane, although convexity can be studied in other spaces, too.
Can you see why the convex polygon in the diagram above is convex? Can you see why the concave polygon is not convex? If not, we'll prove it.
Convex polygons are convex: Suppose \(P\) is a convex polygon. Then, if there exists points \(A,B\) in the polygon such that the line segment \(AB\) is not contained in \(P\), then \(AB\) separates the exterior of \(P\) into multiple regions, including at least one polygon. Call one of these polygons \(Q\). Consider the vertex \(x\) of \(Q\) farthest from the line segment \(AB\) (pick any if there is a tie). Clearly, since \(2\) of the vertices of \(Q\) are on \(AB\), and there are at least \(3\) vertices of a polygon, the vertex \(x\) is not on line segment \(AB\). Thus, it is also a vertex of polygon \(P\). Since all angles of \(P\) have \(\lt180^\circ\), the angle \(x\) in polygon \(Q\) has \(\gt180^\circ\) as it is the exterior angle of \(P\) at vertex \(x\). But this implies that at least one of the two neighboring vertices to \(x\) is farther from \(AB\) than \(x\) is, a contradiction. Thus, if \(P\) is a convex polygon, it is a convex shape.
Concave polygons are not convex: Suppose \(P\) is a concave polygon, with vertices \(A,B,C\) such that \(\angle ABC\) in the polygon has measure \(\gt180^\circ\). Consider the triangle \(\triangle ABC\). Clearly, \(\angle B\) in this triangle is the complement of \(\angle B\) in the polygon, since triangles can't have angles larger than \(180^\circ\). Thus, there exists a point inside \(\triangle ABC\) not contained in polygon \(P\). However, the line segments starting at point \(A\), and ending on points on the line segment \(BC\), go through all the point in the triangle \(\triangle ABC\). Thus, at least one of them is not contained in \(P\), implying that \(P\) is not a convex shape.
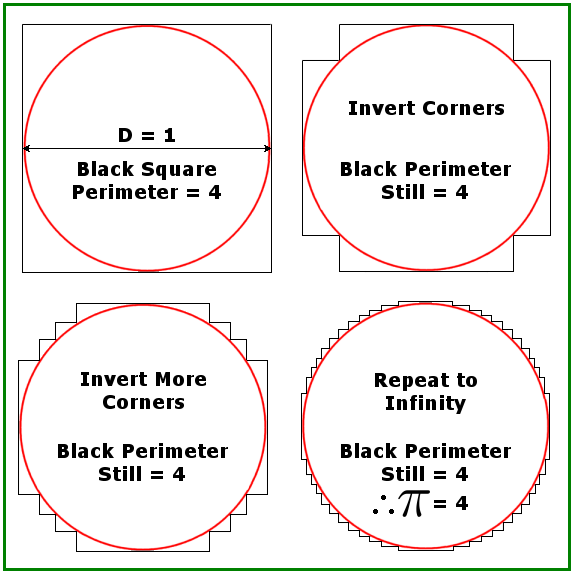
An important application of convexity is perimeter.
Convex Functions
The most common use case of convexity are convex functions.
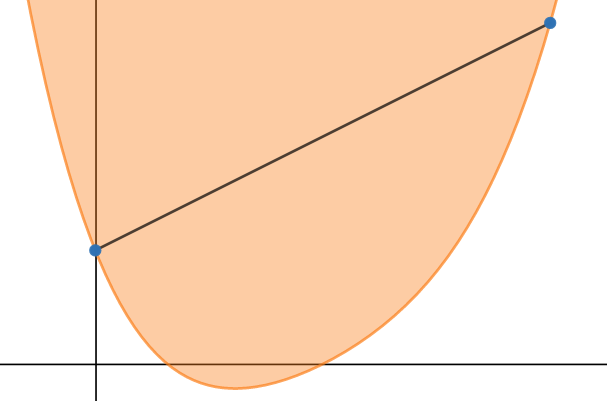
The following function (in dark orange) is an example of a convex function, since the area above the function (in light orange) is a convex shape.
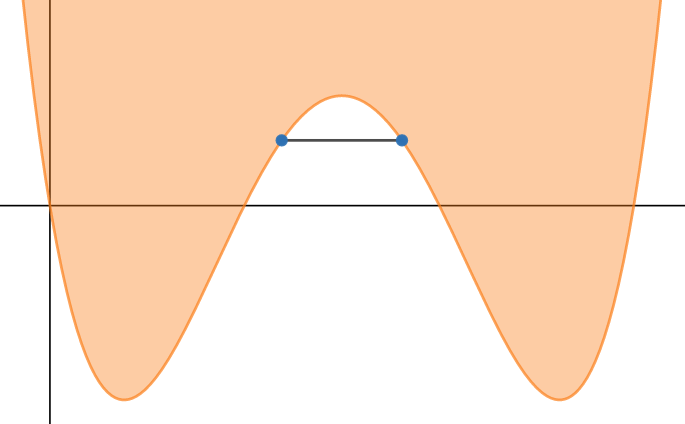
On the other hand, the following function is not convex, as the area above the function is not a convex shape.
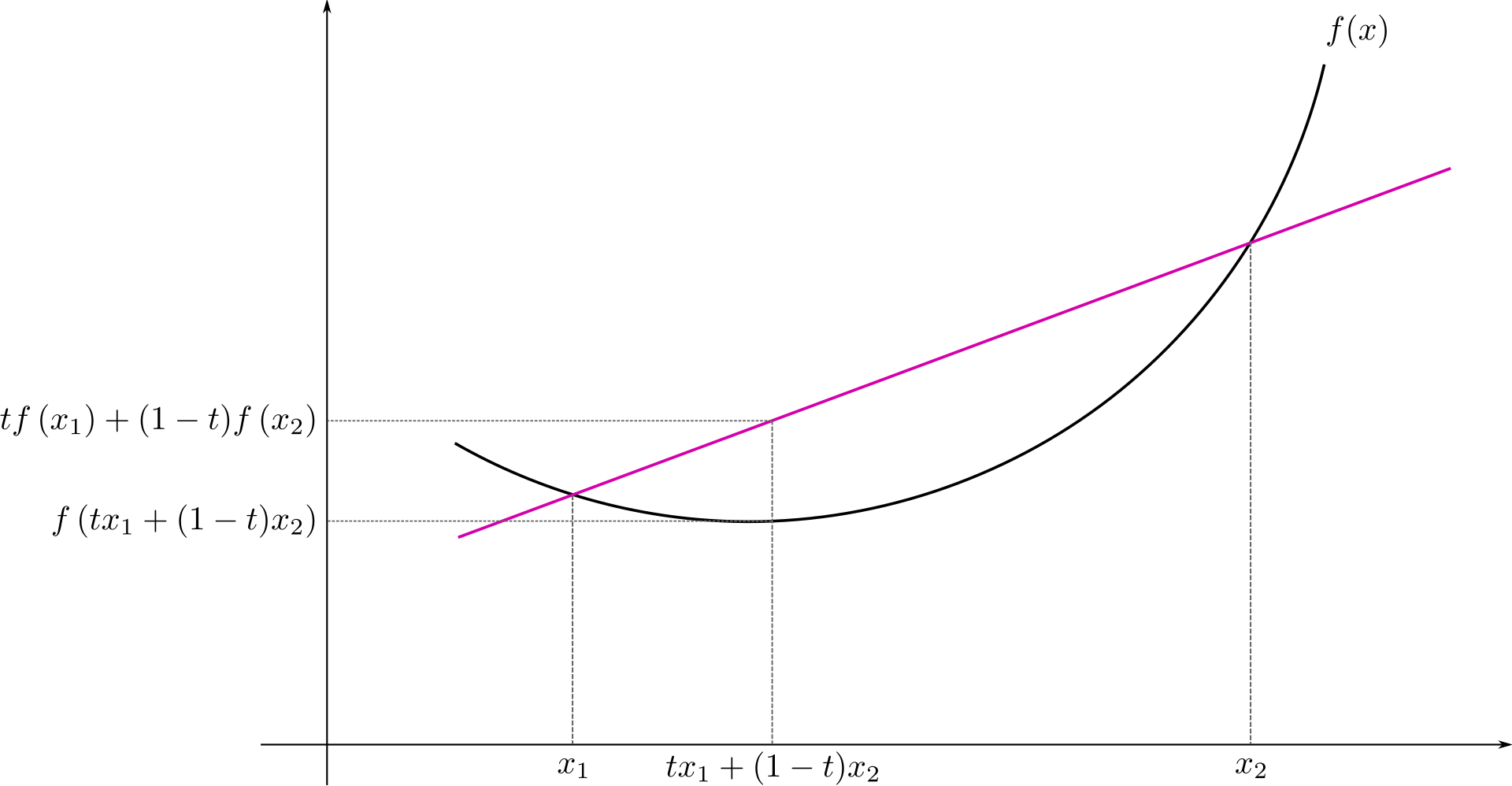
So how do we characterize convex functions? For any numbers \(x_1,x_2\) in the domain of \(f\), if the line segment between points \((x_1,f(x_1))\) and \((x_2,f(x_2))\) is above the function \(f\), then \(f\) is convex, as in the following diagram:
We can write this condition as follows: for any numbers \(x_1,x_2\) in the domain of \(f\) and \(t\in[0,1]\),$$tf(x_1)+(1-t)f(x_2)\geq f(tx_1+(1-t)x_2)$$This inequality, known as Jensen's inequality, is an alternate way to define convex functions. We can also define concave functions to be functions for which the area below the function is convex, or in other words, the negation of convex functions.
- Can you show that a function \(f\) is concave if and only if for all real numbers \(x_1,x_2\) and \(t\in[0,1]\), \(tf(x_1)+(1-t)f(x_2)\leq f(tx_1+(1-t)x_2)\)
- Can you find a function which is neither convex nor concave?
To demonstrate the usefulness of these ideas, we'll prove a famous inequality known as the Arithmetic Mean-Geometric Mean inequality (sometimes written as AM-GM). If you haven't learned about logarithms or induction, I'd suggest waiting till Weeks 12 and 14 before reading any further.
Base Case: \(n=1\): for any positive \(x_1\), \(\ln \frac{x_1}1\geq\frac{\ln x_1}1\)
Inductive Case: Suppose that for any positive \(x_1,\ldots,x_n\), the inequality below holds$$\ln\left(\frac{x_1+x_2+\ldots+x_n}n\right)\geq\frac{\ln x_1+\ln x_2+\ldots+\ln x_n}n$$then, since \(\ln\) is a concave function, for any positive \(a,b\) and \(t\in[0,1]\), \(\ln(ta+(1-t)b)\geq t\ln a+(1-t)\ln b\). Letting \(t=\frac n{n+1}\), \(a=\frac{x_1+x_2+\ldots+x_n}n\), and \(b=x_{n+1}\), a positive number, we get $$\begin{aligned}\ln\left(\frac{x_1+x_2+\ldots+x_{n+1}}{n+1}\right)&\geq\frac n{n+1}\ln\left(\frac{x_1+x_2+\ldots+x_n}n\right)+\frac1{n+1}\ln x_{n+1}\\&\geq\frac n{n+1}\cdot\left(\frac{\ln x_1+\ln x_2+\ldots+\ln x_n}n\right)+\frac{\ln x_{n+1}}{n+1}\end{aligned}$$This completes the proof.
Equality holds for the inequality in AM-GM only when all of the values \(x_1,\ldots,x_n\) are equal. Here's a basic application of the inequality.