\ie\cf
\newcommand{\eqdef}{\mathbin{\stackrel{\rm def}{=}}}  \newcommand{\R} % real numbers  \newcommand{\N}} % natural numbers  \newcommand{\Z} % integers  \newcommand{\F} % a field  \newcommand{\Q} % the rationals  \newcommand{\C}{\mathbb{C}} % the complexes  \newcommand{\poly}}  \newcommand{\polylog}}  \newcommand{\loglog}}}  \newcommand{\zo}{\{0,1\}}  \newcommand{\suchthat}  \newcommand{\pr}[1]{\Pr\left[#1\right]}  \newcommand{\deffont}{\em}  \newcommand{\getsr}{\mathbin{\stackrel{\mbox{\tiny R}}{\gets}}}  \newcommand{\Exp}{\mathop{\mathrm E}\displaylimits} % expectation  \newcommand{\Var}{\mathop{\mathrm Var}\displaylimits} % variance  \newcommand{\xor}{\oplus}  \newcommand{\GF}{\mathrm{GF}}  \newcommand{\eps}{\varepsilon}  \notag
\no
Back to MB3

Week 6 Notes

100%

This week's class is all about volume. Your handout contains a list of common formulas for the volumes of important three-dimensional shapes. Why do these formulas work? How can we derive these formulas ourselves?

The answer to these questions is unfortunate: these formulas must be derived via calculus.

This Week's "Challenge" section won't be difficult, but will rather paint a more general picture of the historical context of how we arrived upon our current understanding of area and volume.

Volume and Surface Area of 3D Shapes

Prisms

We begin our exploration of 3D shapes with prisms. What are prisms?

A prism is a 3D shape formed by taking a 2D shape, and "pushing" it in the third dimension to make a three-dimensional shape. The following image consists of plenty of examples of prisms.

In the image above, you see prisms formed by "pushing" a square, a rectangle, an acute triangle, a right triangle, a circle, and a trapezoid. How do we find the surface area and volume of the prisms?

The volume of a prism is the product of the area of the shape we are pushing, which we call the base, and the length we pushed it, which we call the height.
Given a cylinder with a circle of radius \(r\) as a base, and a height of \(h\), the volume is \(Bh\). \(B\), the area of the base, is \(\pi r^2\). So, the volume of the cylinder is \(\pi r^2h\).
The surface area of a prism is twice the area of the base, plus the height times the perimeter of the base. If \(B\) is the area of the base, \(h\) the height, and \(P\) the perimeter of the base, we have $$2B+hP$$
The perimeter of a circle is \(2\pi r\). So, the surface area is \(2\pi r^2+2\pi rh=2\pi r\cdot(r+h)\)

The definition of the volume of the prism should be pretty self-explanatory. The surface area might be a bit more mysterious. But it too makes sense.

The surface of a prism has three components: the base, the copy of the base which is \(h\) away from the original base, and the side of the prism. It's pretty clear that the surface area of the first two parts is \(2B\).

For the side of the prism, imagine unwrapping the side into a rectangle, as in the following gif.

The height of the rectangle is just the height of the prism. But what is the width of the rectangle? If you watch closely, you'll see that it is just the perimeter of the base.

With this intuition, you shouldn't need to memorize the formulas of surface area and volume of any prism, but instead calculate them on the fly.

Pyramids

The next important class of 3D shapes is Pyramids! What are Pyramids?

A pyramid is a 3D shape formed by taking a 2D shape, and "pushing" it in the third dimension to make a three-dimensional shape. However, unlike prisms, while we push the shape, we also shrink the shape until it is a point at the end of the process.

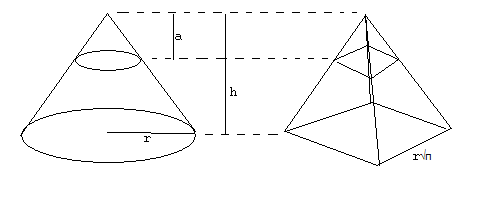
The following diagram consists of 4 pyramids, formed by a hexagon, a circle, a triangle, and a square.

These pyramids are known as hexagonal pyramids, cones, tetraherdons, and square pyramids, respectively. How do you find the volume and surface area of a pyramid?

The volume of a Pyramid with base \(B\) and height \(h\) is \(\frac13Bh\).
Given a cone with a circle of radius \(r\) as the base, and height \(h\), the volume of the cone is \(\frac13Bh=\frac13\pi r^2h\).

This volume formula should seem mysterious. Where is the \(\frac13\) coming from?

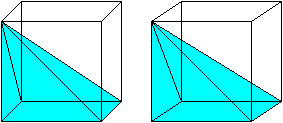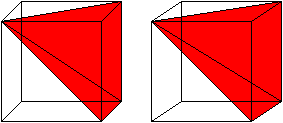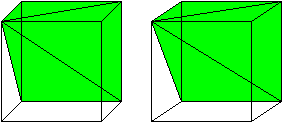
In the case of the right triangular pyramid, there is a nice visual proof of the \(\frac13\) term, which is given by the following gif.

As you can see from the gif, exactly \(3\) copies of this pyramid comprise a rectangular prism with the same base and height as the pyramid. If you can't see it, do the following: click on the gif to expand it. Place a piece of paper between the two cubes so that each of your eyes can only see one cube. Try to cross your eyes so that it looks like one cube. You will "see" the cube and the three embedded pyramids as if they were 3D.

How do we generalize this to all pyramids? We use Cavalieri's Principle. Given any other pyramid, for example a cone, we create a right triangular pyramid with the same height as the other pyramid, and such that the base of the right triangular pyramid has the same area as the other pyramid's base. Here is a diagram where we do this for a cone.

Now for any height \(a\lt h\) as in the diagram, we take a cross section of the other pyramid and the right triangular pyramid. By similarity and the bases having the same area, the two cross sections must have the same area! Thus, the right triangular pyramid and the other pyramid have the same volume by Cavalieri's Principle.

If that confused you, don't worry! We'll talk more about what Cavalieri's principle is and how to think about it later. But for now, this proves the formula for the volume of the pyramid.

Now what about the surface area of a pyramid?

Unfortunately, there is no general formula for this. When the base is a polygon, we can add up the areas of all of the faces of the pyramid to get the surface area. For the cone, the following formula (which I will not prove) gives us the surface area.

Given a cone with base a circle of radius \(r\) and height \(h\), the surface area of the cone is $$\pi r(r+\sqrt{r^2+h^2})$$

This formula is not too important (I haven't seen many questions about the surface area of a cone on any math competitions), but it is one that has to be memorized, until you learn calculus :(.

Sphere

The final important 3D shape is the sphere. How do we compute the volume and surface area of a sphere? We can again apply Cavalieri's Principle!

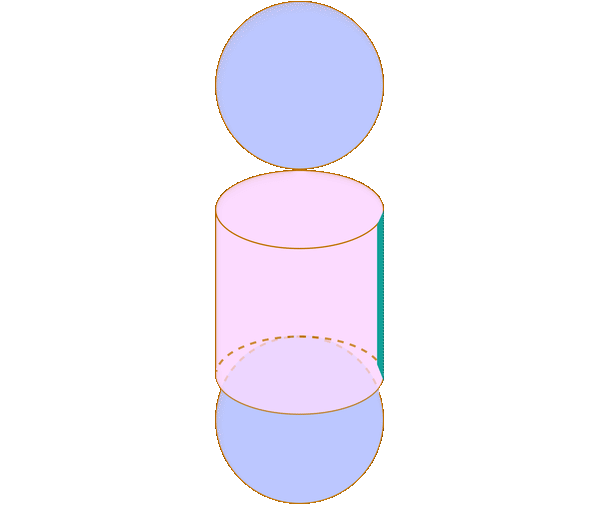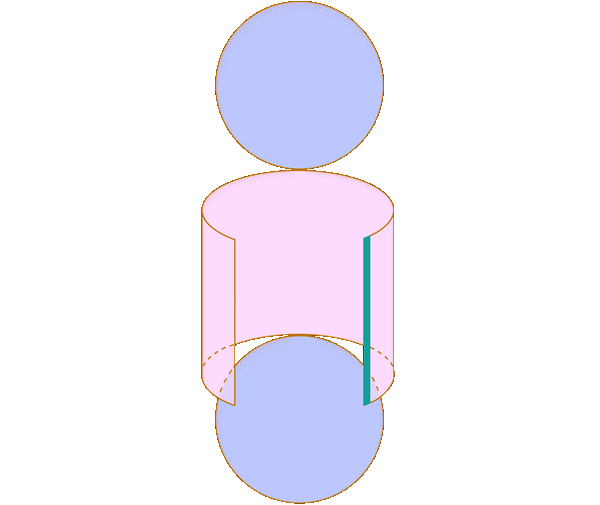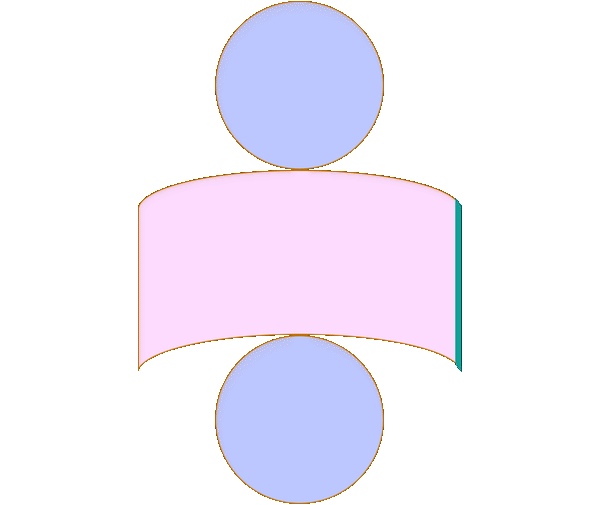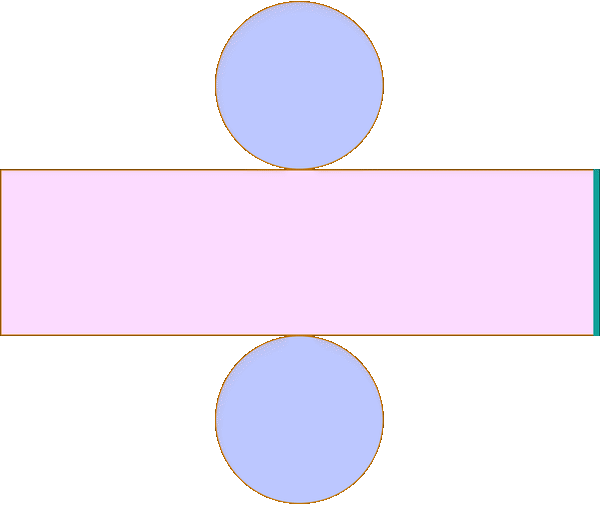
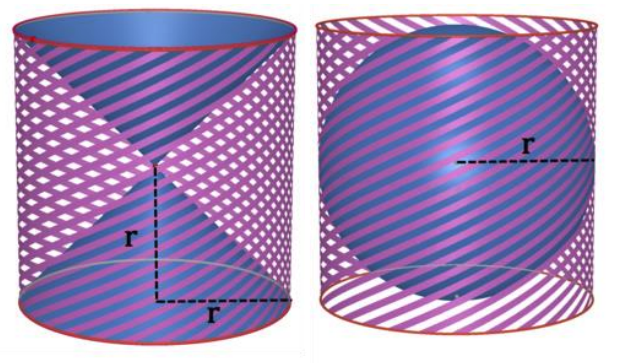
Consider the following diagram.

On the right, you have a sphere with radius \(r\). On the left, you have a cylinder with radius \(r\) and height \(2r\), but with two cones removed from it. Both cones have radius \(r\) and height \(r\).

The volume of the object on the left is something we can calculate with our knowledge so far. The volume of the cylinder is \(\pi r^2\cdot 2r=2\pi r^3\). The volume of either cone is \(\frac13\pi r^2\cdot r=\frac13\pi r^3\). Thus, the volume of the object on the left is $$2\pi r^3-2\cdot\frac13\pi r^3=\frac43\pi r^3$$

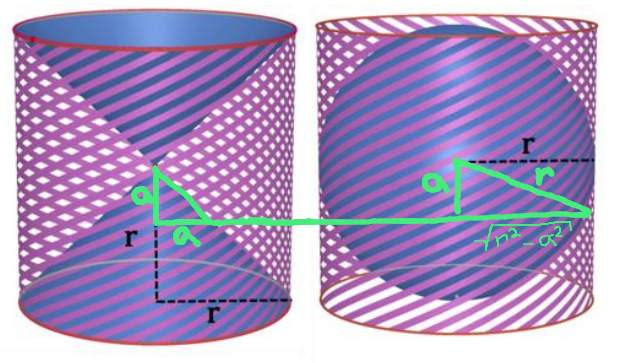
Now we apply Cavalieri's principle. Let's say we pick a cross section of both the object on the left and the sphere \(a\) below the midpoint of the height, as in the diagram below.

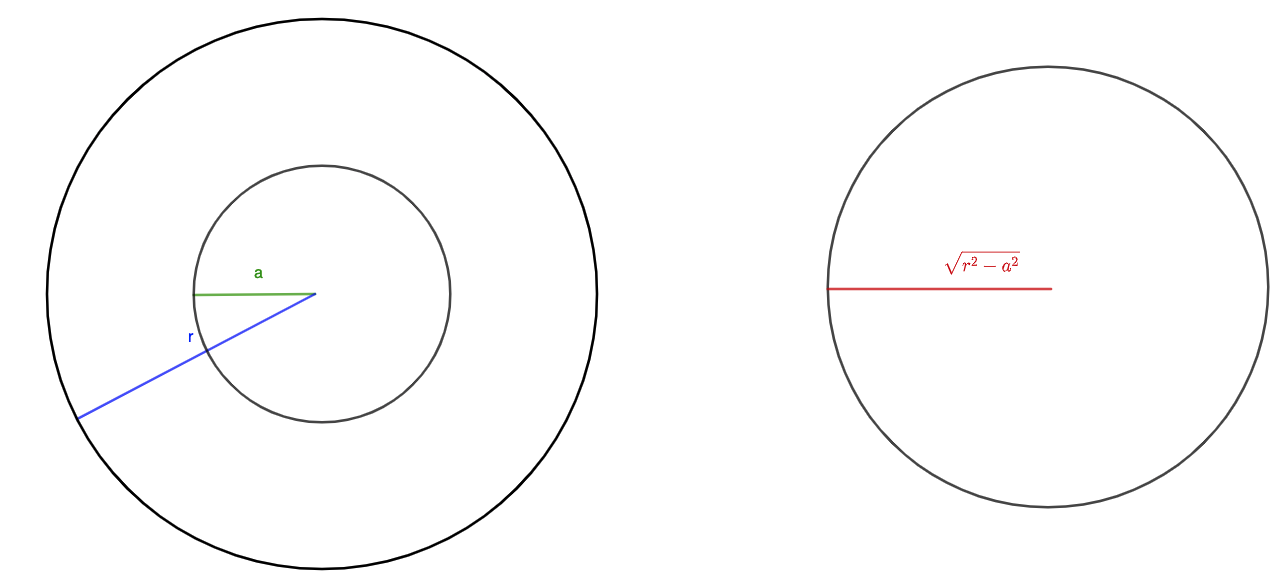
On the left, our cross section is a ring, with outer radius equal to \(r\) (since the radius of the cylinder is \(r\)) and the inner radius equal to \(a\), since the small green triangle on the left is similar to the triangle with \(r\) height and \(r\) length. On the right, the cross section is a circle. Note that in the green triangle on the right, the hypotenuse is the radius of the sphere, which is \(r\). The height is \(a\). Thus, the length (which is the radius of the cross section) is \(\sqrt{r^2-a^2}\) by the Pythagorean Theorem. We draw these cross sections in the following diagram.

The area of the ring on the left is \(\pi r^2-\pi a^2=\pi(r^2-a^2)\). The volume of the circle on the right is \(\pi\left(\sqrt{r^2-a^2}\right)^2=\pi(r^2-a^2)\). Thus, by Cavalieri's Principle, the objects have the same volume since their cross sections have the same area. So, the volume of the sphere is \(\frac43\pi r^3\).

Now how about the surface area? 3Blue1Brown does a far better job explaining how to understand the surface area of the sphere than I ever could. The conclusion is the following:

A sphere with radius \(r\) has surface area \(4\pi r^2\)

Challenge: Why do we need Calculus?

In our discussions about the area of 2D shapes, we've never needed to invoke any ideas of Calculus, but in the section above, we've used Cavalieri's principle, and in the 3Blue1Brown video, the method of exhaustion to find the surface area and volume of important 3D shapes.

These ideas are precursors to the development of calculus, and were later replaced by more general Calculus concepts (Fubini's Theorem and Volume Integrals). But why are these concepts necessary to find volumes of these objects? Is standard geometry not enough?

To answer these questions, we need to take a dive through history.

Method of Exhaustion

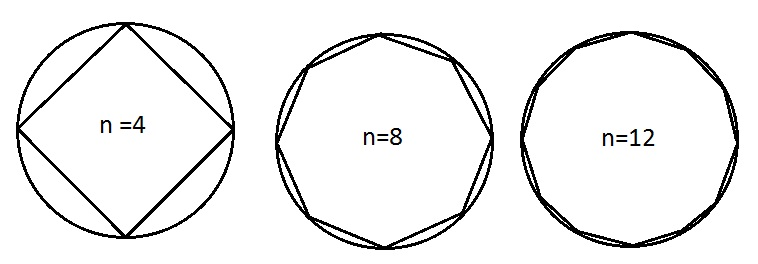
Do you remember this image from the first lecture notes?

This technique of using polygons to approximate a shape, in this case a circle, is known as the method of exhaustion. It was a well-known technique in Ancient Greece for finding the perimeter and area of shapes like ellipses, circles, and other objects using polygons.

The most famous of the methods by exhaustion was called Cavalieri's principle, named after a monk from the 16th century, despite being used by Greek mathematicians much earlier. It says the following:

Given two shapes with the same vertical height, if each horizontal cross section of both shapes has the same length/area, then the shapes have the same area/volume.

This principle, like the other method of exhaustion, should make sense to you. Khan Academy has a nice demonstration of the principle.

One of the earliest documents that we have that mentions the methods of exhaustion is Book XII of Euclid's Elements. Euclid, widely regarded as the father of geometry, dedicates almost the entirety of this book to discussing this technique and all of the things it can do.

Through this book, we can see that Euclid deeply distrusted the method of exhaustion since he was not convinced that the mathematics behind it worked (in fact, he had good reason to doubt it: until the invention of calculus nearly 2000 years later, no mathematician had found a way to explain why it works.)

He also felt that more standard, non-Calculus techniques were sufficient for dealing with shapes with flat sides, like polygons. So how exactly did Euclid deal with area without the method of exhaustion?

Equidecomposability

Euclid preferred thinking about area through the notion of equidecomposability. Here's how it works.

Given any two shapes, they have the same area if I can break one of the shapes into finitely many pieces, rearrange the pieces, and form the other shape. If we can do this process for any two shapes, we call them scissors-congruent. Some examples of scissors-congruent shapes are below.

This idea makes a lot of sense, because if two shapes are made of the same pieces, they have the same area, right?

Euclid believed that this was self-evident. In Elements, he says that it is obvious that any two scissors-congruent shapes have the same area.

He also believed that any two polygons with the same area are scissors-congruent.

Are these ideas true? The answer is yes!

Given any two polygons with the same area, there exists a way to break the first polygon into smaller polygons, rearrange them, and put them back together to make the second polygon.
Given any two shapes in the plane, if I can break one of them into pieces, rearrange them to make the second shape, then the shapes have the same area.

These theorems were proved over 2400 years after Euclid! The Bolyai-Gerwein Theorem was proved in 1833 and von Neumann proved his theorem in 1929.

The Bolyai-Gerwein theorem's proof is possible for you to learn yourself! See this slideshow for an easy explanation.

What's important here is that Euclid's intuition was right: any two scissors-congruent shapes have the same area, and any two polygons that have the same area are scissors-congruent. This means that we don't need calculus when dealing with areas of polygons. Yay!

Into the third dimension!

Euclid's books didn't just talk about perimeter and area, but also surface area and volume! He was of the firm opinion that the methods of exhaustion aren't necessary for dealing with polyhedra, the 3D equivalent of polygons.

A polyhedron is a 3D shape with polygons for faces. Some examples of polyhedra are below.

Euclid claimed the following:

If his claims are true, that would be perfect! We wouldn't need to use calculus to find the volume of any of our shapes (other than the sphere). We could just cut our shapes into pieces, rearrange them into a cube, and prove the volume formulas since we know the volume of a cube.

So are they true?

Story Time!

In 1842, Christian Ludwig Gerling sent a letter to Gauss, excitedly sharing the progress that he and his mentor, Farkas Bolyai, had made on the 3-dimensional version of the Bolyai-Gerwein problem. In this letter, Gerling showed that a mirror-image of a polyhedron is scissors-congruent to the polyhedron.

In 1844, Gauss responded to the letter, expressing dissatisfaction that the volumes of certain polyhedron, including the tetrahedron, still depended on the method of exhaustion/Cavalieri's Principle, rather than the purely geometric idea of scissors-congruence.

In the 1890's, David Hilbert, scouring a library of mathematics, comes upon this correspondence between Gauss and Gerling, finds the ideas interesting, and notes down the 3D Bolyai-Gerwein problem as an interesting problem.

Hilbert, unlike Gauss, was much more negative on the subject. While Gauss believed that it was the limitations of mathematicians that was the reason for them not finding a way to deal with volume without calculus, Hilbert was convinced of the necessity of calculus. He believed that there were two different tetrahedrons with the same volume but that were not scissors-congruent.

Hilbert, in 1900, then went on to publish a list of 28 challenging math problems, which he announced to be the most important math problems that still were unresolved. The third problem was the question "does there exist two tetrahedrons with the same volume but not scissors-congruent"?

Within 6 months of Hilbert publishing his list, his student, Max Dehn, showed that there in fact do exist two tetrahedron that have the same volume but are not scissors-congruent. This, of course, upset many mathematicians.

However, other proofs of the third problem were found to be published far earlier than Dehn's proof.

For example, mathematician Wlayslaw Kretkowski had held a contest for 500 francs (around $10,000) for the solution to the same problem in 1884: 16 years earlier than Hilbert! The award was won by Ludwik Birkemajer, who published a 40 page solution, which predates Dehn's solution by around 15 years.

Unfortunately, Dehn still gets the credit for solving the problem. The world is unfair :(

Banach-Tarski

While many mathematicians were upset by Dehn's result, they still held onto the belief that Euclid's first claim was true: any two scissors-congruent shapes have the same volume.

I mean, of course it is true! If I have a bowling ball, and I cut it into pieces, and rearrange these pieces, I can't just get two bowling balls of the same size, right?

Banach and Tarski disagreed. Their proof in 1924 showed a result which should blow your mind: it is possible to cut a sphere into pieces, rearrange them, and put them together to get two spheres, each with the same volume of the first. That's right, by moving some pieces around, we can double the volume of the sphere.

This result threw away all hope that mathematicians had for equidecomposability as an approach to handling volume. Volume is too weird for geometry, it seems. Calculus it is!

Top