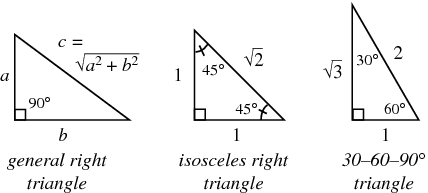\ie\cf
\newcommand{\eqdef}{\mathbin{\stackrel{\rm def}{=}}}  \newcommand{\R} % real numbers  \newcommand{\N}} % natural numbers  \newcommand{\Z} % integers  \newcommand{\F} % a field  \newcommand{\Q} % the rationals  \newcommand{\C}{\mathbb{C}} % the complexes  \newcommand{\poly}}  \newcommand{\polylog}}  \newcommand{\loglog}}}  \newcommand{\zo}{\{0,1\}}  \newcommand{\suchthat}  \newcommand{\pr}[1]{\Pr\left[#1\right]}  \newcommand{\deffont}{\em}  \newcommand{\getsr}{\mathbin{\stackrel{\mbox{\tiny R}}{\gets}}}  \newcommand{\Exp}{\mathop{\mathrm E}\displaylimits} % expectation  \newcommand{\Var}{\mathop{\mathrm Var}\displaylimits} % variance  \newcommand{\xor}{\oplus}  \newcommand{\GF}{\mathrm{GF}}  \newcommand{\eps}{\varepsilon}  \notag
\no
Back to MB3

Week 7 Notes

100%

This week, we'll be learning about Trigonometry! Of course, trigonometry is a vast subject that you will spend nearly a year studying in high school, but we'll try to cover some of the more important results in these notes.

Make sure you have read Week 4's notes before reading these notes.

Given a triangle, any of the three angles in the triangle touch \(2\) of the \(3\) sides. We call the third side the side opposite to the angle.

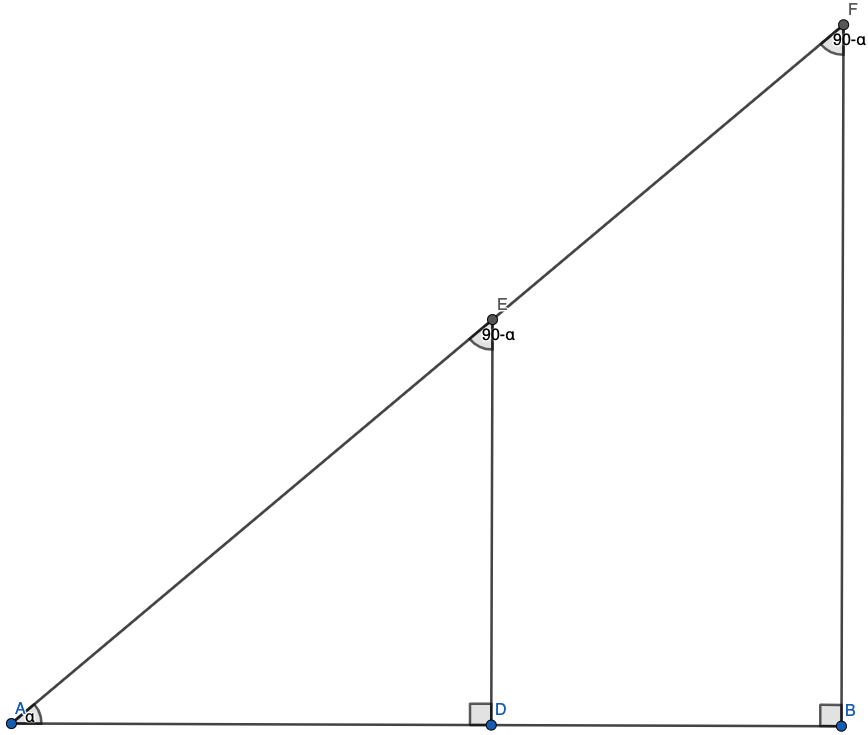
Consider the following right triangles:

Both right triangles share an angle \(\alpha\). Since they both also have a right angle, they are similar by \(AA\). Thus, the ratios of their sides are equal.

In particular, we have \(\frac{ED}{EA}=\frac{BF}{AF}\). \(ED\) and \(BF\) are the opposite sides to \(\alpha\) for their respective triangles, and \(EA\) and \(AF\) are the hypotenuses for the respective triangles.

So as long as the angle is fixed (in this case, \(\alpha\)), the ratio of the opposite side to hypotenuse is the same. This is such an important quantity that we give it a name.

For any angle \(0\lt\alpha\lt\frac\pi2\), draw a right triangle with \(\alpha\) as one of the angles. We define the sine of \(\alpha\), written as \(\sin\alpha\), as the ratio \(\frac{opp}{hyp}\), where \(opp\) is the side opposite to the angle \(\alpha\), and \(hyp\) is the hypotenuse.

From our reasoning earlier, the choice of triangle doesn't matter in calculating the sine. This makes it a very versatile function.

The earliest mentions of the sine function were from the Gupta dynasty in India, with astronomers like Aryabhatta using it to model the trajectories of celestial objects. It was named "jya-ardha" in Sanskrit, meaning "half-chord".This was transliterated as "jiba" in Arabic, but since vowels are often dropped in Arabic, it was often written as "jb". When Arabic texts were translated to Latin in the 12th century, the Gerard of Cremona thought that "jb" stood for "jaib", meaning bosom in Arabic, and chose the most similar word for bosom in Latin: "sinus". Later, this was transliterated into English, giving us "sine".

Given a right triangle, and an acute (\(\lt\frac\pi2\)) angle \(\alpha\) in the triangle, the side which is not opposite to \(\alpha\) and not the hypotenuse is called the side adjacent to \(\alpha\).

Since the triangles in the diagram above are similar, we also know that \(\frac{AD}{AE}=\frac{AB}{AF}\). \(AD\) and \(AB\) are the adjacent sides to \(\alpha\) of their respective triangles, and \(AE,AF\) are the hypotenuses. This again means that the ratio \(\frac{adj}{hyp}\) is independent of the triangle we choose, and only dependent on the value of \(\alpha\). That leads us to the next definition.

For any angle \(0\lt\alpha\lt\frac\pi2\), draw a right triangle with \(\alpha\) as one of the angles. We define the cosine of \(\alpha\), written as \(\cos\alpha\), as the ratio \(\frac{adj}{hyp}\), where \(adj\) is the adjacent side to \(\alpha\).

We now define \(4\) more trigonometric functions which we will use regularly.

Name Notation Definition
Tangent \(\tan\alpha\) \(\frac{\sin\alpha}{\cos\alpha}=\frac{opp}{adj}\)
Cotangent \(\cot\alpha\) \(\frac{\cos\alpha}{\sin\alpha}=\frac{adj}{opp}\)
Cosecant \(\csc\alpha\) \(\frac1{\sin\alpha}=\frac{hyp}{opp}\)
Secant \(\sec\alpha\) \(\frac1{\cos\alpha}=\frac{hyp}{adj}\)

Basic Observations

Now that we have our trigonometric functions, let's make some basic observations.

In our right triangle diagram, observe that the side opposite to \(\alpha\) is adjacent to \(\frac\pi2-\alpha\), and the side adjacent to \(\alpha\) is opposite to \(\frac\pi2-\alpha\). Thus, we have $$\sin\alpha=\cos\left(\frac\pi2-\alpha\right)$$$$\cos\alpha=\sin\left(\frac\pi2-\alpha\right)$$That's certainly a useful observation.

Now given some \(\alpha\), consider \(\sin(\alpha)^2+\cos(\alpha)^2\) (which we write as \(\sin^2\alpha+\cos^2\alpha\)). This equals $$\left(\frac{opp}{hyp}\right)^2+\left(\frac{adj}{hyp}\right)^2=\frac{opp^2+adj^2}{hyp^2}$$But now we use the Pythagorean Theorem! \(opp^2+adj^2=hyp^2\), so $$\sin^2\alpha+\cos^2\alpha=1$$Surprised? Well, what if I told you we actually did this already, in the first week! Don't believe me?

In the first week, we observed that given a Pythagorean triple \(a^2+b^2=c^2\), we could rewrite it as \(\left(\frac ac\right)^2+\left(\frac bc\right)^2=1\). Viewing \(a\) as \(adj\), \(b\) as \(opp\), and \(c\) as \(hyp\) gives us \(\sin^2\alpha+\cos^2\alpha=1\). But this insight is far deeper than you might imagine.

Extending the domain

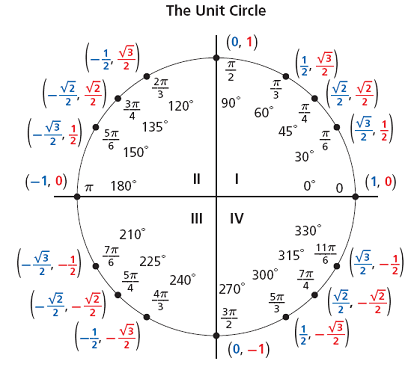
In Week 1, we noticed that \(\left(\frac ac,\frac bc\right)\) can be viewed as a point on the unit circle. With our rewrite, \((\cos\alpha,\sin\alpha)\) can be viewed as a point on the unit circle. As a demonstration of this principle, click on this Desmos graph to see the green point \((\cos\alpha,\sin\alpha)\) as \(\alpha\) varies from \(0\) to \(\frac\pi2\).

Note that the slope of the hypotenuse is \(\frac{\sin\alpha-0}{\cos\alpha-0}=\tan\alpha\), the hypotenuse has length \(1\), and the angle formed by the \(x\)-axis and the hypotenuse is \(\alpha\)! This suggests that we may want to redefine \(\sin\) and \(cos\) as follows:

Given a real number \(\theta\), draw a line segment starting at the origin of length \(1\) such that the angle formed by the positive \(x\) axis and this segment is \(\theta\) (going counter-clockwise). We define \(\sin\theta\) to be the \(y\)-coordinate of the other endpoint of this segment, and \(\cos\theta\) to be the \(x\)-coordinate of the other endpoint.

Check to see that these two definitions of \(\sin\) and \(\cos\) are identical.

The beauty of this new definition is that \(\sin\) and \(\cos\) are now defined for all real numbers, rather than just for \(0\lt\alpha\lt\frac\pi2\). \(\tan\) and \(\sec\) are defined whenever \(\cos\alpha\neq0\), and \(\cot\) and \(\csc\) are defined whenever \(\sin\alpha\neq0\).

If you are still confused by the new definition, see this Desmos graph and watch the relationship between \(\alpha\), the right triangle, and the values of \(\cos\alpha,\sin\alpha\).

With our new definition, prove the following relations for any \(\alpha\): $$\sin(\pi-\alpha)=\sin\alpha,\;\sin(\pi+\alpha)=-\sin(\alpha)$$$$\cos(\pi-\alpha)=-\cos\alpha,\;\cos(\pi+\alpha)=\cos\alpha$$$$\sin(2\pi+\alpha)=\sin\alpha,\;\cos(2\pi+\alpha)=\cos\alpha$$$$\sin(-\alpha)=-\sin\alpha,\;\cos(-\alpha)=\cos\alpha$$
Compute \(\sin\alpha,\cos\alpha\) for the following values of \(\alpha\):
  • \(\alpha=0\)
  • \(\alpha=\frac\pi2\)
  • \(\alpha=\pi\)
  • \(\alpha=\frac{3\pi}2\)


  • \(\sin\alpha=0,\cos\alpha=1\)
  • \(\sin\alpha=1,\cos\alpha=0\)
  • \(\sin\alpha=0,\cos\alpha=-1\)
  • \(\sin\alpha=-1,\cos\alpha=0\)

Trigonometric Laws

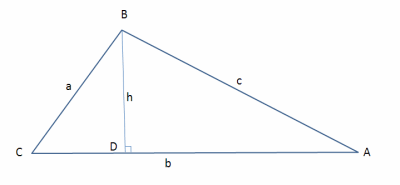
Consider an arbitrary \(\triangle ABC\), and draw an altitude \(h\) from \(B\) to \(AC\).

Call \(\angle BCA\) \(\gamma\). Thus, \(\frac ha=\sin\gamma\), so \(a\sin\gamma =h\). Since \(h\) is an altitude, \(\frac12 bh\) is the area. Substituting in our new formula for \(h\), we have $$\text{Area}=\frac12ab\sin \gamma$$This is a very useful formula. Observe, though, that the choice of \(a,b,c\) doesn't really matter. From Week 4, we have \(\frac{abc}{4R}\) as a formula for the area of a triangle as well. If we call \(\angle BAC\) \(\alpha\) and \(\angle CBA\) \(\beta\), we have $$\frac{abc}{4R}=\frac12ab\sin\gamma=\frac12ac\sin\beta=\frac12bc\sin\alpha$$Dividing all of the equations by \(\frac12abc\) gives us $$\frac1{2R}=\frac{\sin\gamma}c=\frac{\sin\beta}b=\frac{\sin\alpha}a$$This is known as the Law of Sines, as it tells us that the ratio between the sine of an angle and the side opposite to it is constant for any triangle (and only dependent on the circumradius, oddly enough).

Now, observe that \(\cos\gamma = \frac{CD}a\), so \(a\cos\gamma = CD\). Thus, \(b-a\cos\gamma=DA\). But, by the Pythagorean theorem, $$DA^2+h^2=c^2$$Substituting our values for \(h\) and \(DA\) into this formula gives us $$a^2\sin^2\gamma+b^2-2ab\cos\gamma+a^2\cos^2\gamma=c^2$$Since \(\sin^2\gamma+\cos^2\gamma=1\), we have $$a^2+b^2-2ab\cos\gamma=c^2$$This equation is called the Law of Cosines, and is also very useful.

Special Right Triangles

In Week 4, we discussed \(2\) special right triangles

We can use these special triangles to figure out values of \(\sin\) and \(\cos\) for certain angles.

Note that $$\sin30^\circ=\sin\frac\pi6=\cos\frac\pi3=\frac12$$since the side opposite to \(30^\circ\) in the \(30-60-90\) triangle is \(1\) and the hypotenuse is \(2\).

Likewise, $$\sin60^\circ=\sin\frac\pi3=\cos\frac\pi6=\frac{\sqrt3}2$$

And, using the isosceles right triangle, we have $$\sin45^\circ=\sin\frac\pi4=\cos\frac\pi4=\frac1{\sqrt2}$$

We can use the relations in New Relationships to generate the following diagram:

You shouldn't memorize most of the material in this week's notes: rather, you should understand the process by which it is derived, and be confident in your ability to figure out similar problems on the fly.

Remember that an equilateral triangle has three angles, all with measure \(\frac\pi3\). Use the area formulas above to derive the area of an equilateral triangle.

Challenge: Euler's Formula

This section will assume a basic understanding of complex numbers. If you haven't seen them before, I'd suggest just glancing through the conclusions of this section, and ignoring Euler's Formula and the derivations

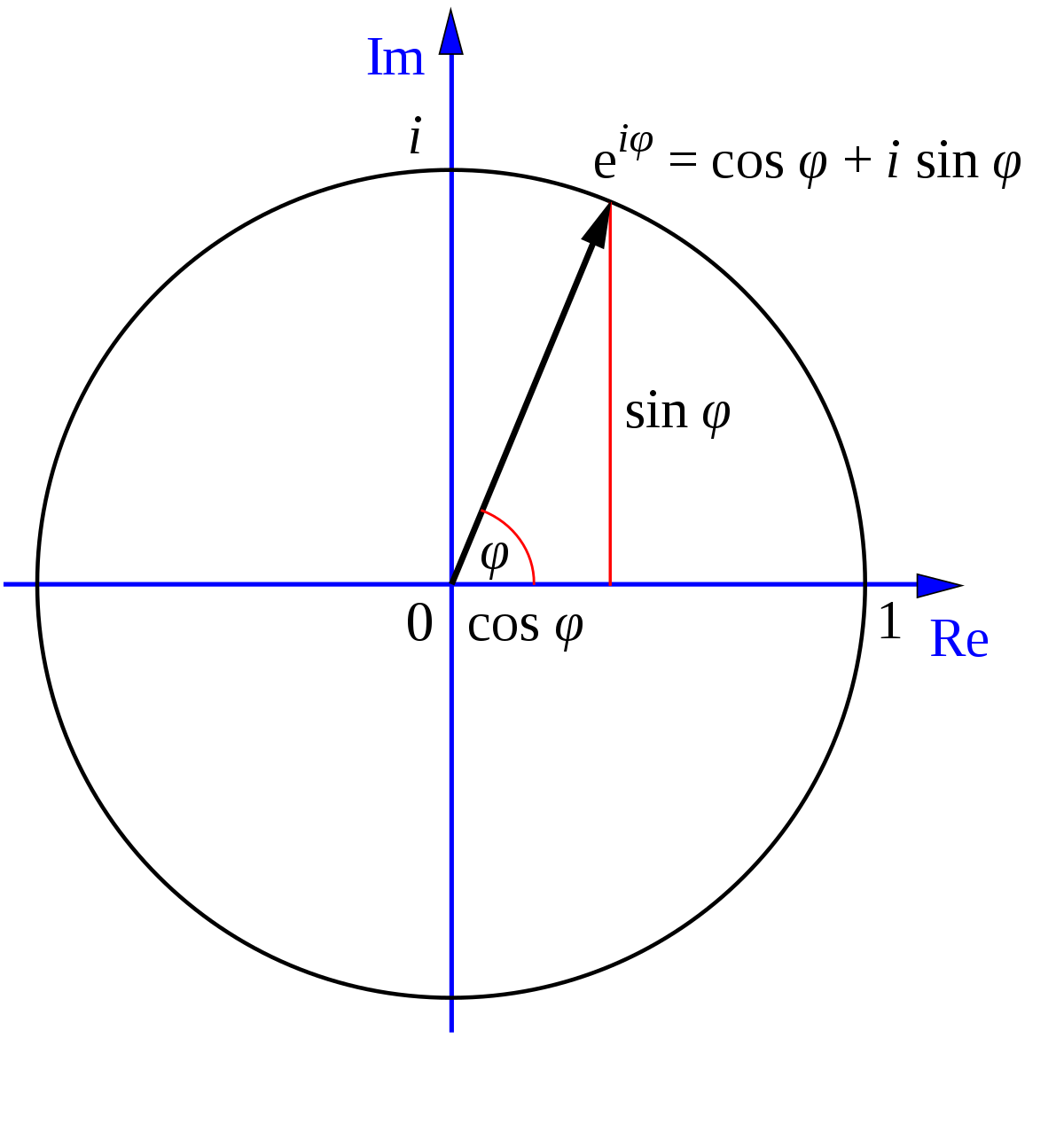
In the previous sections, we viewed \((\cos\theta,\sin\theta)\) as a point on the unit circle in the plane. What if we replaced the plane with the complex numbers? In this case, the \(x\)-axis becomes the real numbers, and the \(y\)-axis the imaginary numbers. In this case, \((\cos\theta,\sin\theta)\) would become \(\cos\theta+i\sin\theta\).

What makes this such a powerful way of representing trigonometric functions is Euler's Formula, widely regarded by mathematicians as one of the most beautiful, if not the most beautiful, formula in all of mathematics.$$e^{i\theta}=\cos\theta+i\sin\theta$$If you don't really understand the formula, or don't get the hype yet, don't worry. We'll work through some of the more basic implications of this formula, although a full study of this formula would take years.

Polar Form

Suppose I have the complex number \(a+bi\). Then, the distance of this complex number from the origin, known as the magnitude of the complex number, is \(\sqrt{a^2+b^2}\). Call this value \(r\). So, we have \(a^2+b^2=r^2\).

As we did above, we divide both sides by \(r^2\). We get $$\left(\frac ar\right)^2+\left(\frac br\right)^2=1$$Thus, we have a right triangle, with \(\frac ar\) as the horizontal leg of the right triangle, \(\frac br\) as the vertical leg of the right triangle, and \(1\) as the hypotenuse. Let \(\alpha\) be the angle of this triangle.

So, \(\cos\alpha=\frac ar\), \(\sin\alpha =\frac br\), so \(r\cos\alpha + ri\sin\alpha=a+bi\). Thus, we can write $$a+bi=re^{i\alpha}$$This way of writing complex numbers is called polar form, since instead of writing the horizontal and vertical components of the complex number, we write the magnitude (how far it is from the origin) and the angle (the angle the line segment from the origin to the number makes with the positive \(x\)-axis).

Now, you may be wondering, why would you bother to do this? The answer is simple: multiplication. Suppose I wanted to multiply complex numbers \(a+bi,\;c+di\). Pretty painful, isn't it? Instead, what if I wanted to multiply \(re^{i\theta}\) with \(se^{i\alpha}\). Easy! We have $$re^{i\theta}\cdot se^{i\alpha}=rs\cdot e^{i(\theta+\alpha)}$$since \(e^a\cdot e^b=e^{a+b}\). This is great, since it tells us that the product of two complex numbers is the complex number with magnitude equal to the product of the magnitudes of the numbers we multiply, and angle equal to the sum of the angles of the numbers we multiply. Cool, huh?

De Moivre's Theorem

Euler's Formula also allows us to compute \(\cos\) and \(\sin\) for some trickier angles.

From Euler's Formula and the new relationships, it should be obvious that $$\cos\theta=\frac{e^{i\theta}+e^{-i\theta}}2,\;\sin\theta=\frac{e^{i\theta}-e^{-i\theta}}{2i}$$But there's a more subtle takeaway from the formula. If \(\mathcal{Re}(a+bi)=a\) and \(\mathcal{Im}(a+bi)=b\) for all complex numbers \(a+bi\), then $$\cos\theta=\mathcal{Re}(e^{i\theta}),\;\sin\theta=\mathcal{Im}(e^{i\theta})$$

We know that $$\cos(\alpha+\beta)+i\sin(\alpha+\beta)=e^{i(\alpha+\beta)}$$$$=e^{i\alpha}\cdot e^{i\beta}=(cos\alpha+i\sin\alpha)(\cos\beta+i\sin\beta)$$$$=\cos\alpha\cos\beta-\sin\alpha\sin\beta+i(\sin\alpha\cos\beta+\cos\alpha\sin\beta)$$Thus, we have $$\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta$$$$\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta$$

Without Euler's Formula, deriving the formulas in the example above would have been much, much more difficult. Let's derive some more formulas!

Use a similar technique to the previous example to find \(\cos(\alpha-\beta)\) and \(\sin(\alpha-\beta)\).
We know that $$\cos(3\alpha+3\beta)+i\sin(3\alpha+3\beta)=e^{3i\alpha}$$$$=(e^{i\alpha})^3=(\cos\alpha+i\sin\alpha)^3$$$$=\cos^3\alpha-3\sin^2\alpha\cos\alpha+i(3\sin\alpha\cos^2\alpha-\sin^3\alpha)$$So, $$\cos(3\alpha)=\cos^3\alpha-3\sin^2\alpha\cos\alpha$$$$\sin(3\alpha)=3\sin\alpha\cos^2\alpha-\sin^3\alpha$$

From this example, we can see that $$\cos(n\alpha)+i\sin(n\alpha)=e^{ni\alpha}=(e^{i\alpha})^n=(\cos\alpha+i\sin\alpha)^n$$This formula is known as De Moivre's Theorem, and is really hard to memorize, but is very easy to remember if we know Euler's Formula.

Using a similar technique to the example above, show that $$\cos(2\alpha)=\cos^2\alpha-\sin^2\alpha$$$$\sin(2\alpha)=2\sin\alpha\cos\alpha$$
Observe that $$\cos\alpha\cos\beta=\frac{e^{i\alpha}+e^{-i\alpha}}2\cdot\frac{e^{i\beta}+e^{-i\beta}}2$$$$=\frac12\cdot\left(\frac{e^{i(\alpha+\beta)}+e^{i(-\alpha-\beta)}+e^{i(\alpha-\beta)}+e^{i(\beta-\alpha)}}2\right)$$$$=\frac12\left(\cos(\alpha+\beta)+\cos(\alpha-\beta)\right)$$
Use the technique from the above example to show that $$\sin\alpha\sin\beta=\frac12\left(\cos(\alpha-\beta)-\cos(\alpha+\beta)\right)$$$$\sin\alpha\cos\beta=\frac12\left(\sin(\alpha+\beta)+\sin(\alpha-\beta)\right)$$

There are so many more formulas that we can derive by playing around with Euler's Formula. What's amazing about it is that all of these formulas are somehow buried in a simple, one-line formula. Now that's a powerful formula.

Top