Week 8 Notes
- Modular Arithmetic
- Addition
- Multiplication
- Division
- Chinese Remainder Theorem
- Challenge: Totient Theorem
This week's notes are about one of the most important topics in all of mathematics. It really is worth taking the time to understand it well.
Modular Arithmetic
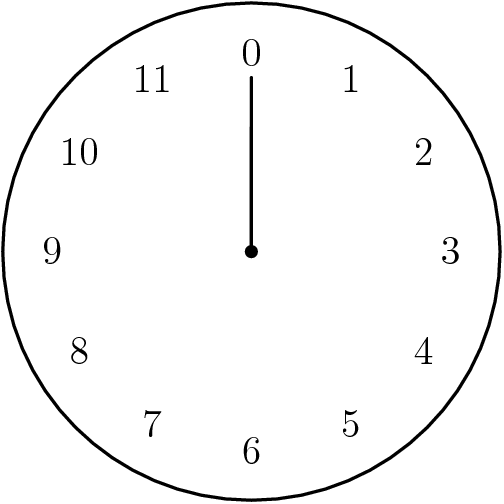
Consider a standard clock, but with the \(12\) replaced by a \(0\).
What time will the clock point to in \(1\) hour? How about \(2\) hours?
Starting at noon, we can see that the hour hand will point to $$1,2,3,4,5,6,7,8,9,10,11,0,1,2,3,4,5,6,7,8,9,10,11,0,\ldots$$in order. If we went backwards in time, the hour hand would go $$11,10,9,8,7,6,5,4,3,2,1,0,11,\ldots$$
This is the way we count in mod \(12\). When we add \(n\), an integer, to \(k\), a number on our clock, we forward time (or go back in time if \(n\) is negative) by \(n\) hours, and see what number the clock will point to if it started at \(k\).
As you might guess, adding \(n+12\) to the clock is the same as adding \(n\) to the clock, since the clock doesn't measure how many rotations it has undergone. Because of this, we say that \(n+12\equiv n\bmod{12}\), or in English, \(n+12\) is equivalent to \(n\) modulo \(12\). All this says is that if I move time ahead by \(n\), it is the same as moving the clock ahead by \(n+12\).
So when are two integers equivalent? They are equivalent when their difference is a multiple of \(12\), since the hour hand points to the same number. In fact, this is how we will define mod.
So by this definition, \(-13\equiv-1\equiv11\equiv23\bmod{12}\). Now, it is the case that every integer \(x\) is equivalent to exactly one non-negative integer \(r\) which is less than the modulus \(n\). We call \(r\) the remainder when \(x\) is divided by \(n\). \(r\) is also called the residue of \(x\) (with \(n\) implicit from the context). In the case of mod \(12\), there are \(12\) possible remainders: \(0,1,\ldots,11\).
- \(x=12,\;n=5\)
- \(x=3,\;n=25\)
- \(x=-4,\;n=3\)
Note that two numbers are equivalent exactly when their remainders are the same. Are you getting the hang of mods yet? Here are some (obvious) properties of equivalence (sometimes also called congruence)
- \(a\equiv a\bmod n\) since \(a-a=0\) and \(0\) is a multiple of all integers.
- If \(a\equiv b\bmod n\), then \(a-b=kn\) for some integer \(k\), so \(b-a=(-k)n\), implying that \(b\equiv a\bmod n\).
- If \(a\equiv b\bmod n\) and \(b\equiv c\bmod n\), then there are integers \(j,k\) such that \(a-b=jn\), \(b-c=kn\). So, \(a-c=a-b+b-c=(j+k)n\). Thus, \(a\equiv c\bmod n\).
Addition
Part of what makes modular arithmetic so useful is that it behaves really well with addition. In particular, we have the following result:
Mods also work well with subtraction, as we show in the next theorem.
So, when we have equivalences, we can add and subtract to either side without worry.
Multiplication
We just learned that mods are well-behaved with addition and subtraction. What about multiplication?
The answer is still yes! This is what truly lends power to modular arithmetic, but we'll see that with some examples.
Since exponentiation is repeated multiplication, it too is preserved by mods. In particular, if \(a\equiv b\bmod n\), then for any non-negative integer \(k\), \(a^k\equiv b^k\bmod n\). This is a very important observation in a common class of problems, an example of which is presented below.
These sorts of "find the remainder when \(a^b\) is divided by \(c\)" problems show up all the time on competitions. In the Challenge Section, I'll present a foolproof way to solving these problems.
Division
Suppose I know that \(ka\equiv kb\bmod n\). Do I know that \(a\equiv b\bmod n\)? On a cursory glance, you might say, of course! Just divide both sides by \(k\).
The issue here is that I don't know what it means to divide by \(k\)! What is \(3\) divided by \(5\)? \(0.6\)? But \(0.6\) is not a valid value in our mod system.
So what does it mean to divide by \(k\)? Well, it means to multiply by \(\frac1k\). \(\frac1k\) is the number such that \(k\cdot\frac1k=1\).
Our question becomes, how do we know such a \(\frac1k\) exists? The answer is, it doesn't always exist. However, if \(\gcd(k,n)=1\), it does exist. This is summarized in the hugely important lemma below.
Let \(n_1=\frac n{\gcd(n,m)}\) and \(m_1=\frac m{\gcd(n,m)}\). So, \(\gcd(n_1,m_1)=1\). Now suppose there exists integers \(0\leq a\lt b\lt k_1\) such that \(m_1a\equiv m_1b\bmod{n_1}\). Then, \(m_1(b-a)\) is a multiple of \(n_1\).
Since \(\gcd(m_1,n_1)=1\), this means that \(b-a\) is a multiple of \(n_1\). Since \(b-a\) is positive, this means that \(b-a\geq n_1\), a contradiction since \(b-a\lt b\lt n_1\).
So, we know that every \(m_1r\) for \(0\leq r\lt n_1\) has a different remainder mod \(n_1\). By the pigeonhole principle, since there are only \(n_1\) possible remainders, there must be some \(r\) for which \(m_1r\equiv1\bmod{n_1}\). That implies that there exists integer \(q\) such that \(rm_1+qn_1=1\).
If this proof was too complicated, don't worry. You won't need it for any competitions. But, for those of you who understood the proof, you'll notice that this lemma gives us no way of finding \(\frac1k\) when \(\gcd(k,n)=1\). So how do we find \(\frac1k\)?
The "easiest" way to find \(\frac1k\) is to use the Extended Euclidean Algorithm, although in most cases, trial and error can be faster than this algorithm.
Thus, we have the following conclusion: if \(ka\equiv kb\bmod n\) and \(\gcd(k,n)=1\), then \(a\equiv b\bmod n\). In essence, this is a limited form of division.
Chinese Remainder Theorem
One of the most important implications of Bezout's Lemma is the Chinese Remainder Theorem. Since it is a large theorem, we will show it in parts. Assume that \(m_1,\ldots,m_r\) are moduli such that for any \(1\leq i\lt j\leq r\), \(\gcd(m_i,m_j)=1\) (we call these numbers pairwise relatively prime). Let \(a_1,\ldots, a_r\) be integers.
This shows that mod \(M=m_1\cdot\ldots\cdot m_r\), there is at most one solution to the system of modulo equivalences. Now, we will show that there is a solution.
For the inductive case, suppose that \(x\) is an integer that satisfies \(x\equiv a_i\bmod{m_i}\) for each \(1\leq i\lt r\). By weakened CRT, there exists an integer \(y\) such that \(y\equiv x\bmod{m_1\cdot\ldots\cdot m_{r-1}}\) and \(y\equiv a_r\bmod{m_r}\). I claim that for all \(1\leq i\lt r\), \(y\equiv a_i\bmod m_i\).
Since \(y\equiv x\bmod{m_1\cdot\ldots\cdot m_{r-1}}\), \(y-x\) is a multiple of this modulus, and thus, \(y-x\) is a multiple of \(m_i\). So, \(y\equiv x\equiv a_i\bmod{m_i}\). This completes the proof.
To summarize, this is the full statement of the Chinese Remainder Theorem.
How do you find this \(x\)? Well, if we follow the proof, we need apply Bezout's Theorem \(r-1\) times, and thus do the Extended Euclidean Algorithm \(r-1\) times. If \(r\) is small or the moduli are small, this is reasonable to do. Otherwise, guess and check is your friend.
Challenge: Totient Theorem
One of Leonhard Euler's many lasting contributions to mathematics is his Totient Function. It is defined as follows for positive integer \(n\): $$\varphi(n)=\text{Number of positive integers } m\lt n\text{ such that }\gcd(m,n)=1$$
For example, \(\varphi(4)=2\), since \(1,3\) are the two numbers below \(4\) relatively prime with \(4\).
How do we compute this for large inputs? We can use the Chinese Remainder Theorem!
Thus, for a positive integer \(n\), we can prime factorize it as \(p_1^{e_1}\cdot\ldots\cdot p_k^{e_k}\). So, we have $$\varphi(n)=\prod\limits_{i=1}^k\varphi(p_i^{e_i})$$Note that $$\varphi(p_i^{e_i})=p_i^{e_i}\cdot\left(1-\frac1{p_i}\right)$$Since there are \(p_i^{e_i-1}\) positive integers below \(p_i^{e_i}\) that have \(p_i\) as a factor.
So, our final formula for the Totient Functions is $$\varphi(n)=n\cdot\prod\limits_{i=1}^k\left(1-\frac1{p_i}\right)$$
Now why do we care about the Totient Function? Well, I promised you earlier that I'd provide a foolproof way of finding multiplicative inverses and solving the problems of the form "what is the remainder when \(a^b\) is divided by \(c\)". The approach depends on the following theorem.
This is a truly beautiful result. It tells us that \(\frac1a=a^{\varphi(n)-1}\). In the case that \(n\) is prime, we have the following result as a direct implication.
In base \(b\), the period of \(\frac pq\) (in simplest form) is the smallest positive integer \(k\) such that there exists a natural number \(n\) with $$b^n\equiv b^{n+k}\bmod q$$\(n\) represents the number of digits before the decimal starts repeating, and \(k\) is the period.
In our problem, we know by Fermat's Little Theorem that \(10^6\equiv10^0\bmod7\), so the period is \(6\).
To find the remainder of \(a^b\) when divided by \(n\), assuming \(\gcd(a,n)=1\), we note that \(a^{\varphi(n)}\equiv1\bmod n\), so if \(c\) is the remainder of \(b\) when divided by \(\varphi(n)\), then \(a^b\equiv a^c\bmod n\). This will simplify the problem to one we can handle.
For a final interesting result that follows from the Totient Theorem, consider the following exercise.
For some context about the name of the last theorem, McDonald's sold its nuggets in boxes of \(9\) and \(20\). So people wondered, what is the largest amount of nuggets that is impossible to get. This sort of problem does occasionally appear on MathCounts.