\ie\cf
\newcommand{\eqdef}{\mathbin{\stackrel{\rm def}{=}}}  \newcommand{\R} % real numbers  \newcommand{\N}} % natural numbers  \newcommand{\Z} % integers  \newcommand{\F} % a field  \newcommand{\Q} % the rationals  \newcommand{\C}{\mathbb{C}} % the complexes  \newcommand{\poly}}  \newcommand{\polylog}}  \newcommand{\loglog}}}  \newcommand{\zo}{\{0,1\}}  \newcommand{\suchthat}  \newcommand{\pr}[1]{\Pr\left[#1\right]}  \newcommand{\deffont}{\em}  \newcommand{\getsr}{\mathbin{\stackrel{\mbox{\tiny R}}{\gets}}}  \newcommand{\Exp}{\mathop{\mathrm E}\displaylimits} % expectation  \newcommand{\Var}{\mathop{\mathrm Var}\displaylimits} % variance  \newcommand{\xor}{\oplus}  \newcommand{\GF}{\mathrm{GF}}  \newcommand{\eps}{\varepsilon}  \notag
\no
Back to MB3

Week 9 Notes

100%

This week is Countdown Week again! As such, the notes will be short, but make sure to review the material from the first 8 weeks.

Aritho-Geometric Sequences

In Week 5, we learned about arithmetic and geometric sequences. But what happens when we combine them?

An Aritho-Geometric sequence is a sequence of terms where each term is the product of an element from an arithmetic series and a geometric series

In other words, if \(a_1,\ldots\) is an arithmetic sequence with common difference \(d\), and \(b_1,\ldots\) is a geometric sequence with common ratio \(r\), then the following is an aritho-geometric sequence$$\frac{a_1}{b_1},\frac{a_2}{b_2},\ldots$$

So how do we evaluate $$S=\sum\limits_{n=1}^\infty\frac{a_n}{b_n}$$Well, let's assume \(r\gt1\) so that this sum is defined. In that case, $$rS-S=\frac{a_1r}{b_1}+{a_2-a_1}{b_1}+{a_3-a_2}{b_2}+\ldots$$But, \(a_{i+1}-a_i=d\), so $$rS-S=\frac1{b_1}\cdot\left(a_1r+d\sum\limits_{n=1}^\infty\frac1{r^n}\right)$$Using our geometric sequence formula, $$b_1(r-1)S=a_1r+\frac{d}{1-1/r}$$$$S=\frac r{b_1(r-1)^2}\cdot(a_1(r-1)+d)$$

Is this the most pleasant formula in the world? No, and I don't suggest memorizing it. But what you should remember from this is the technique used to derive it, since it is useful in summing aritho-geoemtric sequences

Can you find a formula for \(\sum\limits_{n=1}^k\frac{a_n}{b_n}\)? Hint: $$\sum\limits_{n=1}^k\frac{a_n}{b_n}=\sum\limits_{n=1}^\infty\frac{a_n}{b_n}-\sum\limits_{n=k+1}^\infty\frac{a_n}{b_n}$$
Evaluate $$1+2\cdot2+3\cdot2^2+\ldots+100\cdot2^{99}$$


Let \(S\) be the desired sum. Then $$2S=1\cdot2+2\cdot2^2+\ldots+100\cdot2^{100}$$$$S=2S-S=-(1+2+2^2+\ldots+2^{99})+100\cdot2^{100}$$$$S=99\cdot2^{100}-1$$

Telescoping Sums/Products

Sometimes, when evaluating sums or products, we rewrite the terms in such a way that we cancel most terms. This is called telescoping, and is a very useful technique.

The general idea is as follows:$$\sum\limits_{n=1}^k(a_{n+1}-a_n)=a_{k+1}-a_1$$$$\prod\limits_{n=1}^k\frac{a_{n+1}}{a_n}=\frac{a_{k+1}}{a_1}$$The challenge, of course, is figuring out when a sequence can be rewritten in this way.

The best way to understand this technique is with some examples.

Evaluate $$\sum\limits_{i=1}^n\frac1{i(i+1)}=\frac1{1\cdot2}+\frac1{2\cdot3}+\ldots+\frac1{n\cdot(n+1)}$$


Note that for any $a\lt b$, $$\frac1{(k+a)(k+b)}=\frac1{b-a}\left(\frac1{k+a}-\frac1{k+b}\right)$$Letting $k=i$, $a=0$, $b=1$ gives us the sum $$\left(1-\frac12\right)+\left(\frac12-\frac13\right)+\ldots+\left(\frac1n-\frac1{n+1}\right)=1-\frac1{n+1}$$Partial fraction decomposition is a very common technique for generating telescoping series.

The equation used in the solution to the exercise above is known as partial fraction decomposition, and is definitely a technique to remember

Evaluate $$\sum\limits_{i=1}^ni!(i^2+1)$$


Note that $$k!(k^2+1)=k^2\cdot k!+k!$$$$=k(k\cdot k!)+k!$$$$=k((k+1)!-k!)+k!$$$$=k(k+1)!-(k-1)k!$$This telescopes, so the sum is $$n\cdot(n+1)!-0\cdot1!=n\cdot(n+1)!$$

Challenge: Limits

We've seen several infinite sums in this class already, but what does it actually mean to sum infinitely many numbers? In this section, we'll explore what it means precisely.

Sequence limits

Consider the following sequence: $$\frac12,\;\frac23,\;\frac34,\;\frac45,\ldots$$The general form of this sequence is \(\frac n{n+1}\). Intuitively, we can see that the terms of this sequence are approaching \(1\). How can we make this idea precise?

We can play a game. Pick any \(\varepsilon\gt0\). Can we find a natural number \(n\) such that all terms after the $n$th term are in the interval \((1-\varepsilon,1+\varepsilon)\)? The answer is yes! Find some natural number \(n\) such that \(n\gt\frac1\varepsilon\). Then, \(\frac1{n+1}\lt\varepsilon\), so \(1\gt\frac n{n+1}\gt1-\varepsilon\).

In other words, regardless of how small we make \(\varepsilon\), there is a point in the sequence such that the distance of the terms of the sequence from \(1\) is less than \(\varepsilon\). We say that this sequence limits towards \(1\), or in mathematical notation, $$\lim\limits_{n\to\infty}\frac n{n+1}=1$$

Can you figure out what the following means?$$\lim\limits_{n\to\infty}f(n)=\infty$$


It means the following: for any \(\varepsilon>0\), there exists a natural number \(n\) such that for any natural \(m\gt n\), \(f(m)>\varepsilon\). In other words, the sequence will eventually be bigger than any finite value.

Infinite Sums

So how do limits help us define infinite sums? We define infinite sums as follows:$$\sum\limits_{n=1}^\infty f(n)=\lim\limits_{m\to\infty}\sum\limits_{n=1}^mf(n)$$In other words, it is the limit on \(n\) of the sums of the first \(n\) terms.

Finite Limits

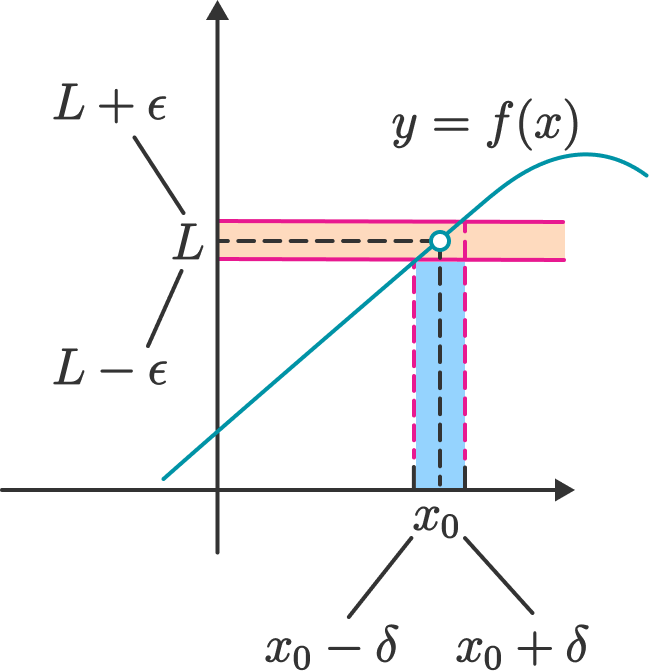
We can generalize limits over functions. To understand this, visualize an exchange between two parties, Alice and Bob. First, Alice challenges Bob, "I want to ensure that the values of \(f(x)\) will be no farther than \(\varepsilon \gt 0\) from \(L\)." If the limit is indeed \(L\), then Bob will be able to respond by giving her a value of \(\delta\), "If for all points \(x\) is within a \(\delta\)-radius interval of \(x_0\), then \(f(x)\) will always be within an \(\varepsilon\)-interval of \(L\)." If the limit exists, then Bob will be able to respond to Alice's challenge no matter how small she chooses \(\varepsilon\).

For example, in the graph for function \(f(x)\) below, if Alice gives Bob the value \(\varepsilon\), then Bob gives her the number \(\delta\) such that for any \(x\) in the open interval \(( x_0 - \delta, x_0 + \delta )\), the value of \(f(x)\) lies in the interval \(( L - \varepsilon, L + \varepsilon)\). In this example, as Alice makes \(\varepsilon\) smaller and smaller, Bob can always find a smaller \(\delta\) satisfying this property.

If there is any value of \(\varepsilon\) for which Bob cannot find a corresponding \(\delta\), then the limit does not exist!

If the limit exists, we write $$\lim\limits_{x\to x_0}f(x)=L$$

Prove that $$\lim\limits_{x\to\infty}\frac1{x^2}=0$$


Alice picks some \(\varepsilon\gt0\). What value of \(\delta\) can Bob pick so that any real number \(x\gt\delta\) satisfies \(\frac1{x^2}\in(0-\varepsilon,0+\varepsilon)\)? Well, if Bob picks \(\delta=\frac1{\sqrt\varepsilon}\), then if \(x\gt\delta\), $$0\lt\frac1{x^2}\lt\frac1{\delta^2}=\varepsilon$$Thus, Bob won the game, and that proves the limit.
Let \(f(n)=\frac1{2^n}+\frac1{3^n}+\ldots\). Compute $$\sum\limits_{n=2}^\infty f(n)$$


Compute $$\frac14\cdot\frac25\cdot\ldots\cdot\frac{50}{53}$$

Compute $$\sum\limits_{n=1}^\infty\frac{3n-1}{2^n}$$

Prove that if there is a perfect square in an arithmetic sequence of positive integers, there are infinitely many squares in that arithmetic sequence.

The geometric sum $$a+ar+\ldots=7$$and$$ar+ar^3+ar^5+\ldots=3$$Compute \(a+r\).
Top