Abelian Categories
If you've survived the drawl that was the first \(5\) parts of this chapter, congratulations! There shouldn't be any more terminology dumps on this blog (I hope?), and we can finally do some math (Some may argue that the proof of Yoneda's lemma is "math", but in my opinion, the lemma is just a rephrasing of the definition of categories, rather than a novel observation).
In this post, we'll be defining abelian categories, which have a technical definition, but can be thought intuitively as categories that behave similarly to \(Mod_A\).
Additive Categories
- \(\Mor(A,B)\) has a binary operation \(+\) such that \(\Mor(A,B)\) is an abelian group. We call the identity element \(0_{AB}\).
- \(\circ:\Mor(B,C)\times\Mor(A,B)\to\Mor(A,C)\) is a bilinear mapping (linear on each input).
- There exists a zero-object \(0\in\mathfrak C\).
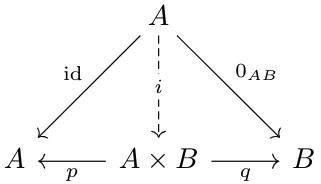
- There exists \(A\times B\in\mathfrak C\) (not necessarily unique, but unique up to isomorphism, as seen in a previous post).
For additive categories, we rename \(\Mor\) to \(\Hom\), representing sets of homomorphisms. An additive functor is a functor \(F\) such that for all \(A,B\), \(F(A\times B)=F(A)\times F(B)\).
Properties of additive categories/functors:
- If \(Z\) is the zero-object, then \(|\Hom(Z,Z)|=1\), so the sole element must be the identity map, which also is \(0_{ZZ}\). And, if \(\id_Z=0_{ZZ}\), then by property \(2\):$$0\circ f=(0+0)\circ f=0\circ f+0\circ f$$so \(0\circ f=0\) for all \(f\) and dually, \(f\circ0=0\). But, $$0=0\circ f=\id\circ f=f$$This implies that the homomorphism groups \(\Hom(Z,A),\;\Hom(A,Z)\) for any \(A\) are trivial, so \(Z\) is the zero-object. Thus, \(Z\) is a zero object iff \(\id_Z=0_{ZZ}\).
- For any objects \(A,B\in\rmA\), and additive functor \(F:\mathfrak A\to\mathfrak B\), \(F\) induces a group homomorphism \(\Hom(A,B)\to\Hom(F(A),F(B))\) via \(f\mapsto F(f)\). Thus, \(F(0_{ZZ})=0_{F(Z)F(Z)}\), and \(F(\id_Z)=\id_{F(Z)}\). Thus, zero objects are mapped to other zero objects.
- The first bullet unintentionally proves that \(0\circ f=f\circ 0=0\) for any morphism \(f\) and for any \(0\) morphism. This necessarily implies that \(0_{AB}=A\to0\to B\), where \(0\) is a zero-object, and \(A\to0\) and \(0\to B\) are the unique morphisms in \(\Hom(A,0)\) and \(\Hom(0,B)\). In fact, it's convenient to define \(0_{AB}\) this way for categories with zero objects.
- Additive categories also have coproducts. In fact, products and coproducts (as long as they are finite) are isomorphic! This will be proven below. This is why the finite product of abelian groups and finite direct sum of abelian groups are isomorphic.
- Fibered products have a simple characterization in abelian categories: Given \(a: X\to Z\), \(b: Y\to Z\), and letting \(c:X\times Y\cong X\sqcup Y\to Z\) induced by \(a,-b\), \(X\times_ZY\cong\ker c\). For the dual, given \(a:Z\to X\), \(b:Z\to Y\), and \(c:Z\to X\times Y\) induced by \(a,-b\), \(X\sqcup_ZY\cong\cok c\).
- \(Mod_A\) is additive. All the properties are pretty easy to verify so it is left to the reader.
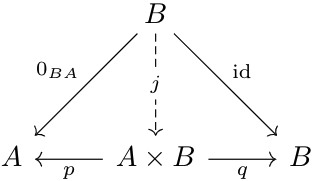
And likewise, let \(j:B\to A\times B\) be defined by the product diagram below:
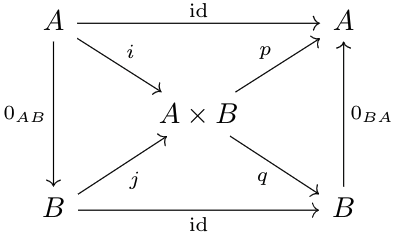
Then, we can draw the following commutative diagram:
This diagram is essentially the two previous diagrams glued together. Now, consider some \(W\in\mathfrak A\) with morphisms \(\alpha:A\to W\), \(\beta: B\to W\) and let $$\phi=\beta\circ q+\alpha\circ p:A\times B\to W$$Note that $$\phi\circ i=\beta\circ q\circ i+\alpha\circ p\circ i=\beta\circ0+\alpha\circ\id=\alpha$$And \(\phi\circ j=\beta\).
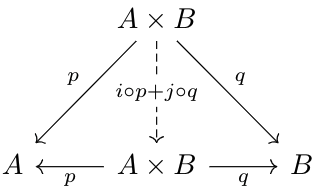
Next, observe that the following diagram commuting implies that \(i\circ p+j\circ q=\id_{A\times B}\).
As hinted upon earlier in our remarks, we can actually define the direct sum as the product endowed with the morphisms \(i,j\) as defined above. It's not hard to see that \(i,j\), and the product fully determine \(p,q\), so some definitions endow the direct sum with all \(4\) maps.
(Co)kernels
The categorical notion of a kernel generalizes the algebraic notion of kernels, by defining them as the largest object that gets mapped to \(0\) by a morphism.
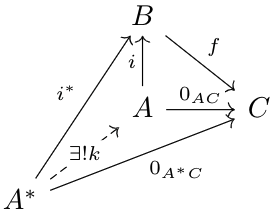
Let \(\mathfrak C\) be a category with a zero-object called \(0\). For some morphism \(f:B\to C\), the kernel is an object \(A\) paired with an inclusion \(i:A\hookrightarrow B\) such that \(f\circ i=0\), and for any other object \(A^*\) with map \(i^*\) with the aforementioned properties, there exists a unique map \(k:A^*\to A\) such that \(i^*=i\circ k\) (you should recognize this as the standard universal property trick to ensure uniqueness of the kernel). In diagram form, we have
and similarly, we can define the cokernel as the colimit of the reversed diagram. I chose not to define quotient spaces earlier on (which probably lead to some rather tedious work-arounds) since quotient objects can be defined strictly as cokernels of additive categories.
Kernel maps are often indicated by \(\hookrightarrow\) or \(\rightarrowtail\). Cokernel maps are often indicated by \(\twoheadrightarrow\).
- Kernels in categories with zero objects (and thus \(0\)-morphisms) are monomorphisms. For any kernel \(k:K\to A\) of \(f:A\to B\), and for any \(g:C\to K\), observe that \(f\circ k\circ g=0\), so by the universal property of the kernel, \(g\) is unique. By an identical argument, cokernels are epimorphisms.
- The kernel map (if it exists) is the \(0\) map iff \(f\) is a monomorphism (this should make sense: what is the kernel of an injection?). For one direction, note that $$f\circ\ker f=0=f\circ 0$$and since \(f\) is a monomorphism, \(\ker f=0\). For the other, observe that for any \(g,h\) with \(f\circ g=f\circ h\), \(f\circ(g-h)=0\). So, if \(f\circ i\neq0\) for all \(i\neq0:C\to A\), then \(f\) is a monomorphism. Now for any map \(i:C\to A\), if \(f\circ i=0\), by the kernel property, there exists a map \(k:C\to0\) such that \(i=k\circ l\), where \(l\) is the kernel morphism. \(k=0\), so \(i=0\). This shows \(f\) is a monomorphism.
This argument in the dual proves that the cokernel map is the \(0\) map iff \(f\) is an epimorphism. When \(f\) is a monomorphism, we say that \(A\) is a subobject of \(B\). When \(f\) is an epimorphism, we say \(B\) is a quotient object of \(A\).
Abelian Categories
As our tangent on kernels and cokernels showed us, kernels (cokernels) are monomorphisms (epimorphisms) if they exist. But we might ask the reverse question: are all monomorphisms (epimorphisms) kernels (cokernels) of some map? In the study of abelian groups, this is the case, and is known as the first isomorphism theorem of group theory. Abelian categories are defined to generalize this concept.
- Every morphism has a kernel and cokernel
- Every monomorphism is the kernel of some morphism (i.e., monomorphisms are normal).
- Every epimorphism is the cokernel of some morphism (i.e., epimorphisms are normal).
Some terminology/facts used in abelian categories for a morphism \(f:A\to B\):
- The image of \(f\) is defined by \(\im(f)=\ker(\cok(f))\). Likewise, the coimage of \(f\) is defined as \(\coim(f)=\cok(\ker(f))\).
- As mentioned earlier, if \(f\) is a monomorphism, the cokernel is called the quotient. We notate \(\cok(f)\) as \(B/A\).
Some important results to show the power of these conditions:
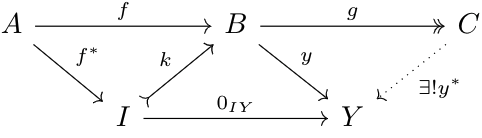
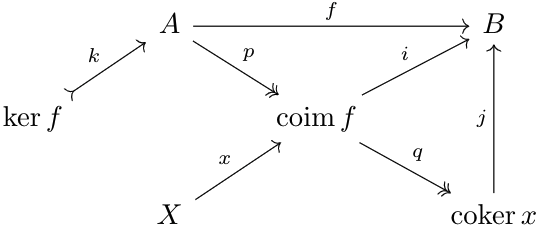
Let \(k=\ker f\), \(p=\cok(k)=\coim f\). Thus, since \(p\) is the cokernel of \(k\), and \(f\circ k=0\), there exists a unique \(i:\coim f\to B\) such that \(i\circ p=f\). We've seen earlier that if for any \(x: X\to\coim f\), \(i\circ x=0\) implies \(x=0\), then \(i\) is monic. Let \(x\) be such a map. Let \(q:\coim f\to\cok x\) be the cokernel of \(x\). By the same argument as above, there exists a unique \(j: \cok x\to B\) such that \(i=j\circ q\). We can summarize these results in the diagram below:
Since epimorphisms are preserved under composition, \(q\circ p\) is epimorphic, and thus, there exists a morphism \(h:C\to A\) such that \(q\circ p=\cok h\). So, $$f\circ h=j\circ q\circ p\circ h=0$$By the kernel properties of \(k\), there exists a unique \(h^*\) such that \(h=k\circ h^*\). Thus, $$p\circ h=p\circ k\circ h^*=0\circ h^*=0$$By the cokernel properties of \(q\circ p\), there exists a unique \(p^*\) such that \(p=p^*\circ q\circ p\). Since \(p\) is epimorphic, we have \(p^*\circ q=\id\). Thus, \(q\) is monic, and since we have \(q\circ x=0\), that implies \(x=0\), so \(i\) must be monic.
Dually, the induced map \(j:A\to\im f\) is epic.
Let \(j:A\to\im f\) be defined as in Lemma 3. Thus, $$f\circ\ker f=\im f\circ j\circ \ker f=0$$Since we showed in Lemma 1 that \(\im f\) is monomorphic, \(j\circ\ker f=0\). Thus, since \(\coim f\) is the cokernel of \(\ker f\), there exists a unique \(f^*\) such that \(f^*\circ\coim f=j\).
But, \(A\to\im f\) being epic and \(\coim f\to B\) being monic implies \(f^*\) is epic and monic, which by Lemma 2 implies that \(f^*\) is an isomorphism. Thus, the image object, with the new coimage map being \(f^*\circ c\) (where \(c\) was the coimage map \(A\to\coim f\)), satisfies the properties of the coimage and thus can be considered to be the coimage. Thus, we often refer to the image as both the image and coimage, and impart both of their properties onto \(\im f\).Since finite products exist by definition, consider the following objects in \(\rmC\): $$D=\prod\limits_{j\in\obj J}F(j),\; R=\prod\limits_{\alpha:i\to j\in\Mor J}F(j)$$\(D\) is the product of all objects mapped to by the functor, \(R\) is the product of all codomain objects of morphisms mapped to by the functor.
Let \(d_j:D\to F(j)\) and \(r_\alpha:R\to F(j)\) refer to projection maps (where \(\alpha:i\to j\in\Mor J\)).
For all \(\alpha:i\to j\in\Mor J\), let \(g_\alpha:D\to F(j)\) be the morphism \(F(\alpha)\circ d_i-d_j\). By the definition of product, there exists a unique morphism \(g:D\to R\) such that for all \(\alpha\), \(g_\alpha=r_\alpha\circ g\). Let \(k:K\to D\) be the kernel of \(g\).
I claim that \(K\), with projection maps \(K_j=d_j\circ k\), satisfies the universal property of the limit. For each \(\alpha:i\to j\in\Mor J\), $$F(\alpha)\circ K_i=F(\alpha)\circ d_i\circ k=g_\alpha\circ k+d_j\circ k=d_j\circ k=K_j$$
And, if there exists an object \(E\), with projection maps \(E_j\) that satisfies \(F(\alpha)\circ E_i=E_j\) for all \(\alpha:i\to j\in\Mor J\), then by product properties, there exists a unique map \(e:E\to D\) such that for all \(j\), \(d_j\circ e=E_j\). And, for all \(\alpha:i\to j\in\Mor J\),$$g_\alpha\circ e=F(\alpha)\circ d_i\circ e-d_j\circ e=F(\alpha)\circ E_i-E_j=E_j-E_j=0$$By product properties, this implies that \(g\circ e=0\). By kernel properties of \(k\), there exists a unique map \(h:E\to K\) such that \(e=k\circ h\). This completes the proof of \(K\) being the limit of \(F\). The dual proof shows all finite colimits exist.Examples
All but the first example are non-abelian, as we'll encounter important examples of abelian categories later.
- \(Mod_A\) for any commutative ring \(A\) is abelian. This construction would be pointless otherwise.
- Consider the subcategory of \(Mod_\mathbb R\) consisting of just the spaces of even dimension. The map \(f:\mathbb R^2\to\mathbb R^2\) given by \((a,b)\mapsto(a,0)\) is a morphism on this category, but it has no kernel. This category is additive but not abelian.
- Ring is not additive, since it doesn't have a zero-object.
- The category of torsion free abelian groups is additive but not abelian. Consider the map \(\phi:\mathbb Z\to\mathbb Z\), \(\phi(n)=2n\). Suppose \(\phi\) has a cokernel \(f:\mathbb Z\to X\) in the category. Thus, \(f\circ\phi=0\). In particular, \(f(2)=0\). So, \(f(1)+f(1)=0\), and since \(X\) is torsion-free, \(f(1)=0\), which implies that \(X=\{0\}\). Thus, if the cokernel of \(\phi\) exists, it is \(\mathbb Z\to0\). But that's an issue, since the kernel of the map \(\mathbb Z\to\mathbb Z\) is \(\id_{\mathbb Z}\), which would imply that \(\phi\) is not monic, a contradiction.