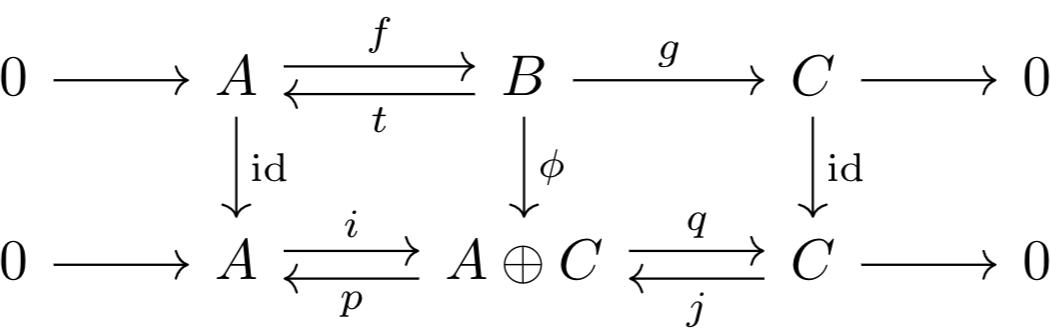\ie\cf
\newcommand{\eqdef}{\mathbin{\stackrel{\rm def}{=}}}  \newcommand{\R} % real numbers  \newcommand{\N}} % natural numbers  \newcommand{\Z} % integers  \newcommand{\F} % a field  \newcommand{\Q} % the rationals  \newcommand{\C}{\mathbb{C}} % the complexes  \newcommand{\poly}}  \newcommand{\polylog}}  \newcommand{\loglog}}}  \newcommand{\zo}{\{0,1\}}  \newcommand{\suchthat}  \newcommand{\pr}[1]{\Pr\left[#1\right]}  \newcommand{\deffont}{\em}  \newcommand{\getsr}{\mathbin{\stackrel{\mbox{\tiny R}}{\gets}}}  \newcommand{\Exp}{\mathop{\mathrm E}\displaylimits} % expectation  \newcommand{\Var}{\mathop{\mathrm Var}\displaylimits} % variance  \newcommand{\xor}{\oplus}  \newcommand{\GF}{\mathrm{GF}}  \newcommand{\eps}{\varepsilon}  \notag
\no
Next |
| Previous

(Co)homology and Exactness

100%

In this post, we'll generalize the notions of homology, cohomology, and exactness from contexts of differential geometry, algebra, or wherever else you've seen it to abelian categories.

Exactness

Given some sequence of objects and morphisms$$\ldots\to A\xrightarrow fB\xrightarrow gC\to\ldots$$

we say that the sequence is a complex at \(B\) if \(g\circ f=0\). If you come from a differential geometry context, you may be more familiar with the term closed. If a sequence is a complex everywhere, we call it a complex sequence. We say that the sequence is exact at \(B\) if \(\ker g=\im f\) (more precisely, there exists a map \(\im f\to B\) which is a kernel map of \(g\)). An exact sequence is a sequence that is exact everywhere. The following result shouldn't be surprising.

If a sequence is exact at \(B\), it is a complex at \(B\).


As observed in the previous post, \(f\) can be factored into a map \(f^*:A\to\im f\) and a kernel map \(k:\im f\to B\). So, $$g\circ f=g\circ k\circ f^*$$\(g\circ k=0\), so that completes the proof.

A short exact sequence is an exact sequence with \(5\) terms, with the first and last being \(0\) (essentially, replace the \(\ldots\) with \(0\) in the sequence above).

Basic Examples:

  • The sequence $$0\to A\xrightarrow fB$$is exact iff \(f\) is a monomorphism. In particular, if \(B=0,\;A=0\). Likewise, the sequence $$A\xrightarrow fB\to0$$is exact iff \(f\) is an epimorphism.
  • A classic short exact sequence is defined for any non-trivial principal ideal \(\langle k\rangle\subset R\), where \(R\) is a commutative integral domain:$$0\to R\xrightarrow{\times k}R\to R/\langle k\rangle\to0$$We can generalize as follows: given any monomorphism \(f:A\to B\) with cokernel \(g:B\to C\), observe that \(g\) is an epimorphism and \(g\circ f=0\). Thus, the following is a short exact sequence:$$0\to A\xrightarrow fB\xrightarrow gC\to0$$Likewise, given epimorphism \(g\), we can generate the same exact sequence by letting \(f=\ker g\).
Given an exact sequence $$0\to A\xrightarrow fB\xrightarrow gC\to0$$The following statements are equivalent:
  1. There exists a map \(t:B\to A\) such that \(t\circ f=\text{id}_A\).
  2. There exists a map \(r:C\to B\) such that \(g\circ r=\text{id}_C\).
  3. There exists an isomorphism \(h:B\to A\oplus C\) such that \(h\circ t\) is one of the embedding maps in the coproduct diagram of \(A\oplus C\) and \(r\circ h^{-1}\) is one of the projection maps in the product diagram of \(A\oplus C\).


    4. Let \(i:A\to A\oplus C\), \(j:C\to A\oplus C\), \(p:A\oplus C\to A\), \(q:A\oplus C\to C\) be the maps defining \(A\oplus C\).

    • \((3\Longrightarrow1,2)\): Let \(t=p\) and \(r=j\). The results follow naturally.

    • \((1\Longrightarrow3)\): By the product properties of \(A\oplus C\), there exists a morphism \(\phi:B\to A\oplus C\) such that \(p\circ\phi=t\), \(q\circ\phi=g\). I claim that the following is a chain morphism of short exact sequences (chain morphisms will be defined properly in the next post).

      Observe that $$p\circ\phi\circ f=t\circ f=\text{id}_A$$so \(p\) is the left inverse of \(\phi\circ f\), which means that by uniqueness, \(\phi\circ f=i\). This shows that the commutative diagram holds, and thus, this is a chain morphism of short exact sequences. We'll show this in the next post, but in a chain morphism between short exact sequences, if the left and right morphisms are isomorphisms, so is the middle. Thus, \(B\cong A\oplus C\).
    • \((2\Longrightarrow3)\): Essentially the same as the last part, except using the coproduct notion of \(A\oplus C\) rather than the product one. If this isn't clear, you should do it as an exercise (it is very similar to the proof above).

    (Co)homology

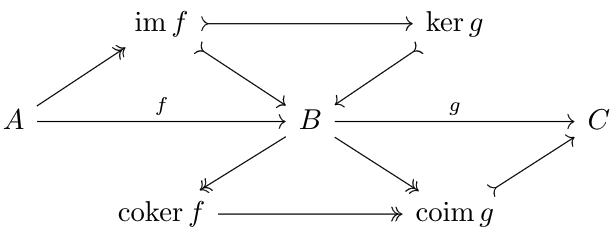
    Let's consider the following complex sequence.$$\ldots\to A\xrightarrow fB\xrightarrow gC\to\ldots$$The homology of the sequence at \(B\) is $$\cok(\im f\to\ker g)=\ker g/\im f$$

    The homology is isomorphic to \(\ker(\cok f\to\coim g)\).


    The diagram induces a sequence $$A\to\im f\xrightarrow i\ker g\xrightarrow jB\xrightarrow p\cok f\xrightarrow q\coim g\to C$$such that the composition equals \(g\circ f=0\). Since \(A\to\im f\) is epic and \(\coim g\to C\) is monic, we can strip them off the sequence to get $$\im f\xrightarrow i\ker g\xrightarrow jB\xrightarrow p\cok f\xrightarrow q\coim g$$ whose composition equals \(0\). So, we have the diagram:

    Since \(q\circ p\circ j=0\) as \(j\) is the kernel of \(q\circ p\), by the kernel properties of \(v\), there exists a unique map \(y\) satisfying the diagram above. Likewise, since \(p\circ j\circ i=0\) as \(p\) is the cokernel of \(j\circ i\), by the cokernel properties of \(u\), there exists a unique map \(x\) satisfying the diagram above. And, $$0=p\circ j\circ i=v\circ x\circ i$$since \(v\) is monic, \(x\circ i=0\). Thus, by the cokernel properties of \(u\), there exists a unique morphism \(z:\cok i\to\ker q\) that satisfies \(z\circ u=x\). By the dual argument, there exists a unique morphism \(z^*:\ker q\to\cok i\) such that \(v\circ z^*=y\). Thus, \(z\circ z^*\) and \(z^*\circ z\), by uniqueness, must be identity morphisms, and thus, \(\ker q\) and \(\cok i\) are isomorphic. This shows the equivalence of our notions of homology.

    Thus, exactness is equivalent to the homology being trivial. We call the elements of \(\ker g\) (assuming that category is concrete) cycles and the elements of \(\im f\) boundaries, as the standard pedagogical example of homology is that of homology groups of simplicial complexes.

    There are two types of complex sequences we are especially interested in:

    • A chain complex is a complex sequence of the following form: $$\ldots\to A_n\to A_{n-1}\to\ldots\to0$$
    • A cochain complex is a complex sequence of the following form: $$0\to\ldots\to A_n\to A_{n+1}\to\ldots$$

    Generally, for a chain complex \(A^*\), we define \(H_i(A^*)\) as the homology at \(A_i\). We define \(H^i(A^*)\) identically if it is a cochain complex, but we call it cohomology instead.

    Factoring Long Complex Sequences

    An infinite exact sequence is sometimes called a long exact sequence if it is infinite. Likewise, a (co)chain complex is sometimes called long if it is infinite. Long sequences can be tough to deal with, so we try to factor long sequences into short ones.

    Consider the following cochain complex:$$A^*:\qquad\ldots\xrightarrow{}A^{i-1}\xrightarrow{f^{i-1}}A^i\xrightarrow{f^i}A^{i+1}\xrightarrow{f^{i+1}}\ldots$$We will construct short exact sequences which represent the data of the complex.

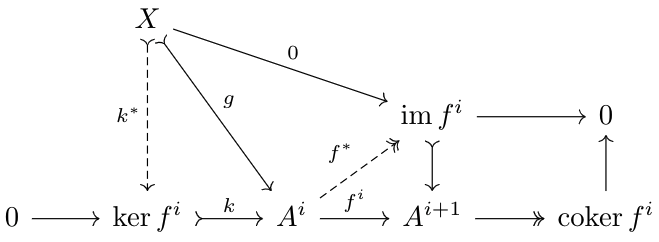
    Let \(k\) be the kernel of \(f^i\), \(f^*:A^i\to\im f^i\) the unique morphism satisfying \(f^i=\im f\circ f^*\), and \(g:X\to A^i\) some morphism such that \(f^*\circ g=0\). Thus, $$0=\im f\circ f^*\circ g=f^i\circ g$$so by kernel properties of \(k\), there exists a unique \(k^*\) such that \(g=k\circ k^*\). Since this works for any \(g\), this shows that \(k\) is a kernel for \(f^*\), so \(\ker f^*=\ker f^i\). But, \(k\) is a monomorphism, so \(\im f^i=\ker f^i\). Thus, we have \(\ker f^*=\im k\). These results are summarized in the diagram below:

    As \(k\) is monic and \(f^*\) is epic, we have the following short exact sequence:$$0\to\ker f^i\xrightarrow{k}A^i\xrightarrow{f^*}\im f^i\to0$$This is an interesting short exact sequence, but it doesn't contain any information regarding the cocycle condition (the condition that requires the composition of adjacent maps to be \(0\)), as it only involves one morphism from the original cochain complex. Let's construct another short exact sequence to encode that information.

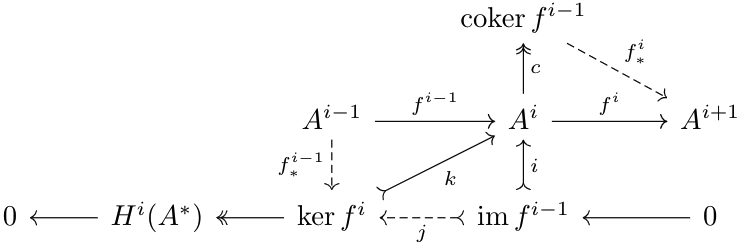
    Since \(f^i\circ f^{i-1}=0\), if \(k:\ker f^i\to A^i\) is the kernel of \(f^i\) and \(c:A^i\to\cok f^{i-1}\) is the cokernel of \(f^{i-1}\), then there exists a unique \(f^{i-1}_*:A^{i-1}\to\ker f^i\) and a unique \(f^i_*:\cok f^{i-1}\to A^i\) such that \(f^{i-1}=k\circ f^{i-1}_*\) and \(f^i=f^i_*\circ c\). If \(i:\im f^{i-1}\to A^i\) is the kernel of \(c\) (and thus the image of \(f^{i-1}\)), then $$f^i\circ i=f^i_*\circ c\circ i=f^i_*\circ0=0$$Thus, by the kernel properties of \(k\), there exists a unique morphism \(j:\im f^{i-1}\to\ker f^i\) such that \(k\circ j=i\). Since \(k,i\) are monic as they are kernels, so is \(j\). These observations are summarized in the diagram below:

    By the second basic example of a short exact sequence, the following sequence is a short exact sequence.$$0\to\im f^{i-1}\xrightarrow j\ker f^i\to H^i(A^*)\to0$$By duality, we also have the following short exact sequences:$$0\to\im f^i\to A^{i+1}\to\cok f^i\to0$$$$0\to H^i(A^*)\to\cok f^{i-1}\to\im f^i\to0$$If \(A^*\) is exact at \(A^i\), i.e., \(H^i(A^*)=0\), then our exact sequences become$$0\to\ker f^i\to A^i\to\ker f^{i+1}\to0$$$$0\to\im f^{i-1}\xrightarrow{\text{id}}\ker f^i\to0$$The latter sequence has no content, so we are left with one short exact sequence.