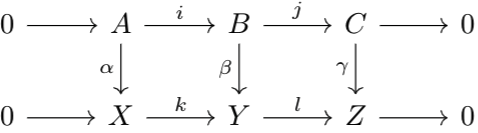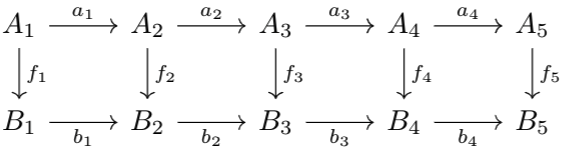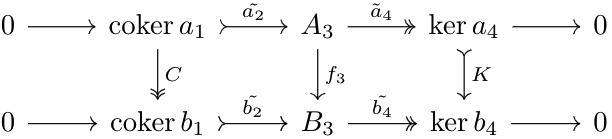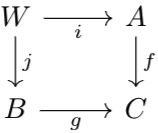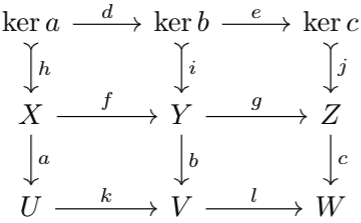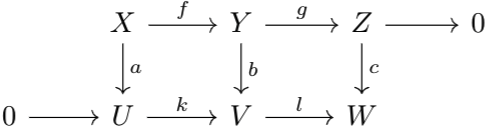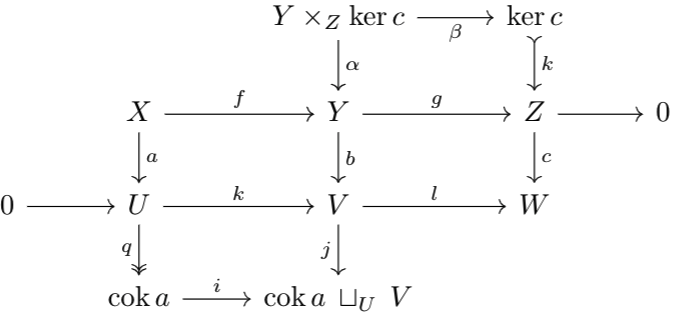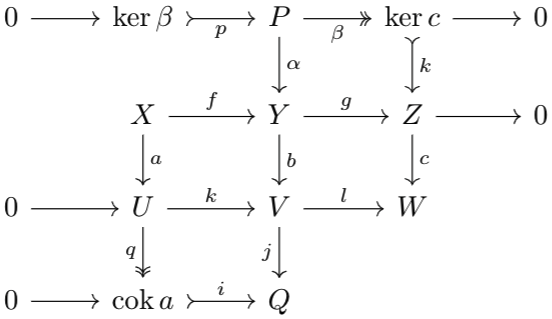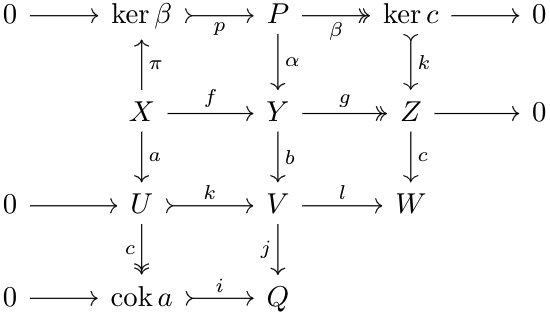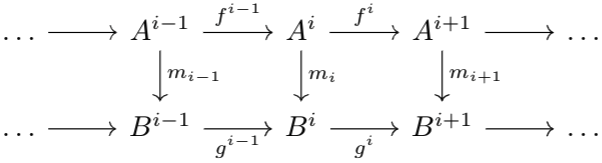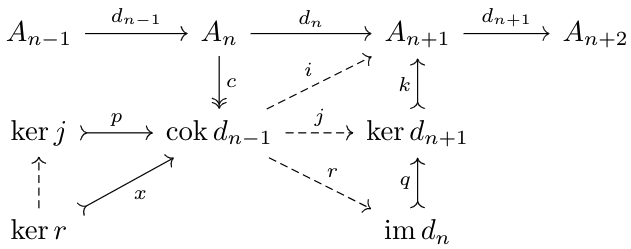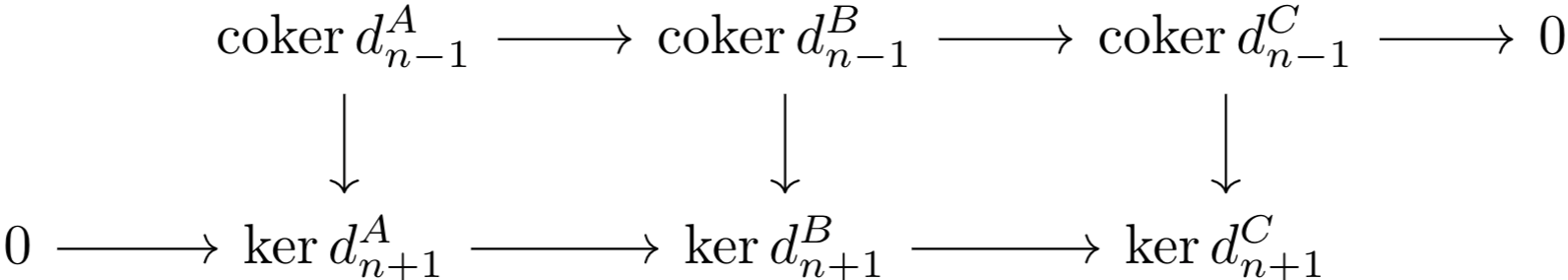Next |
| Previous

(Co)chain Morphisms

100%

What is a chain morphism?

In the previous post, we proved a result involving a chain morphism. A chain morphism is quite simple: Given two complex sequences of the same structure (both finite with the same length, both chain complexes, both cochain complexes, etc), a chain morphism is a morphism between objects in the complex sequences (with each object mapped to a unique object in the other sequence) that commutes with the complex sequence's morphisms.

Chain Morphisms on finite (co)chain complexes

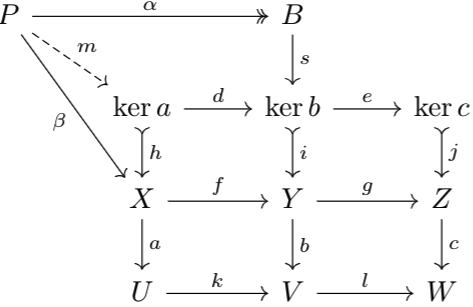
Consider the following diagram, consisting of a chain morphism between two short exact sequences:

Suppose we removed \(\alpha\) from the diagram and asked whether there exists a unique \(\alpha\) satisfying the diagram. Interestingly, the answer is yes! And, the answer to the same question with \(\gamma\) is also yes. In particular, if \(\beta,\gamma\) are isomorphisms, so must be \(\alpha\) (to see why, consider the diagram formed with \(\beta^{-1},\gamma^{-1}\), which by universal property generates a map \(\alpha^{-1}\) by uniqueness. The same logic holds if \(\alpha,\beta\) are given as isomorphisms). But, it isn't true for \(\beta\). Consider the following diagram:

However, we can say something about \(\beta\) given sufficient conditions on \(\alpha,\gamma\).

If \(\alpha,\gamma\) are monic (epic) in the short exact sequence chain morphism diagram, then \(\beta\) is monic (epic).


Note that there is a natural monomorphism \(\chi:\ker\beta\to\ker(l\circ\beta)\) by the kernel properties of \(\ker(l\circ\beta)\) (\(\chi\) is monic since $$\ker\beta=\ker(l\circ\beta)\circ\chi$$and \(f\circ g\) being monic implies \(g\) is monic). And, $$\ker(l\circ\beta)=\ker(\gamma\circ j)\cong\ker j=\im i=i$$since \(\gamma\) is monic. So, we have a natural monomorphism \(\phi:\ker\beta\to A\). In particular, this implies that $$0=\beta\circ\ker\beta=\beta\circ i\circ\ker\beta$$This implies that there exists a unique morphism \(\psi:\ker\beta\to\ker(\beta\circ i)\) that satisfies $$\ker(\beta\circ i)\circ \psi=\ker\beta$$ $$\ker(\beta\circ i)=\ker(k\circ\alpha)\cong\ker k=0$$since \(\alpha\) is monic. Thus, \(\ker\beta=0\), and \(\beta\) is monomorphic.

The dual argument (with kernels replaced with cokernels, and with the bottom exact sequence instead of the top) shows that \(\beta\) is an epimorphism when \(\alpha,\gamma\) are epic.
This doesn't imply that \(\beta\) exists: the example above contradicts this. But, it implies that if \(\beta\) exists, it is monic (epic).

Not all exact sequences are short, so we want to generalize this concept to arbitrary exact sequences.

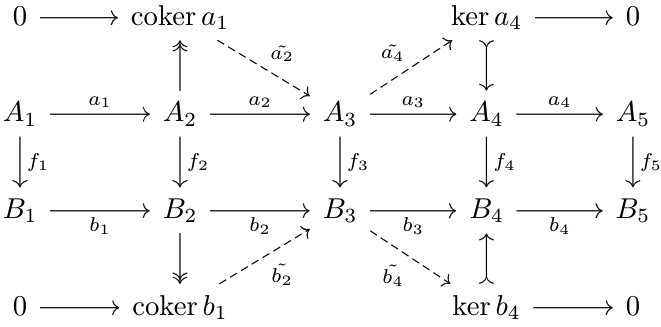
Given the following chain map of exact sequences, if \(f_2,f_4\) are isomorphisms, \(f_1\) is epic, and \(f_5\) is monic, \(f_3\) is an isomorphism.


Observe that by basic kernel/cokernel properties, we arrive upon the following diagram.

What needs to be shown is that the sequence $$0\to\cok a_2\to A_3\to\ker a_4\to0$$ (and likewise for \(B\)) is exact, and that there exist morphisms \(C:\cok a_1\to\cok b_1\) and \(K:\ker a_4\to \ker b_4\) that commute with this diagram.

First, let's show exactness. Observe that \(\cok a_1=\coim a_2\), which implies that \(\coim a_2\to A_3\) is monomorphic, and \(\ker a_4=\im a_3\), so \(A_3\to\im a_3\) is epimorphic by a result proved in Lemma \(4\) of Abelian Categories. Let \(k_A\) be the map \(\ker a_4\to A_4\) and \(c_A\) the map \(A_2\to\cok a_1\). Thus, we have $$0=a_3\circ a_2=c_A\circ\tilde{a_4}\circ\tilde{a_2}\circ k_A$$Since \(k_A\) is monic, and \(c_A\) is epic, we have \(\tilde{a_4}\circ\tilde{a_2}=0\), proving exactness.

Next, observe that $$c_B\circ f_2\circ a_1=c_B\circ b_1\circ f_1=0$$so by cokernel properties, there exists a map \(C:\cok a_1\to\cok b_1\) such that the diagram is satisfied. By a dual argument, there exists a map \(K:\ker a_4\to\ker b_4\) that satisfies the diagram. Note that by symmetry, we can define \(C^*:\cok b_1\to\cok a_1\) and \(K^*:\ker b_1\to\ker a_1\) by swapping all \(A\)s with \(B\)s and vice versa in the argument above. Thus, \(C\circ C^*:\cok b_1\to\cok b_1\) is a unique map satisfying the diagram. But, \(\id\) satisfies the diagram, so \(C\circ C^*=\id\). By a parallel argument, $$C\circ C^*,C^*\circ C,K\circ K^*,K^*\circ K=\id$$thus, \(C,K\) are both isomorphisms. So, we have the following diagram:

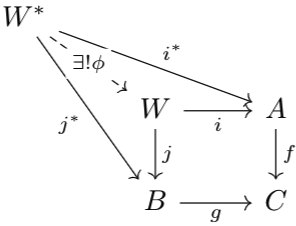
Theorem 1 concludes the proof since \(C,K\) are both isomorphisms.

The next proof (the snake lemma) is very long, so I'll prove \(5\) lemmas before proving the main result. As a reminder, given morphisms \(f:A\to C\), \(g:B\to C\), a cartesian square is an object \(W\), paired with morphisms \(i:W\to A\), \(j:W\to B\), along with \(f,g\) that satisfy the square below, such that (the standard universal property formulation) for any \(W^*\), \(i^*:W^*\to A\), \(j:W^*\to B\), that also satisfy the square as shown in the diagram below, there exists a unique morphism \(\phi:W^*\to W\) which factors \(i^*,j^*\) in terms of \(i,j\). The cocartesian square is the dual notion.

For Lemmas \(1-3\), let the following diagram commute. Additionally, let \((h_1,h_2)\) for morphisms \(h_1:X\to Y\), \(h_1:X\to Z\) refer to the induced morphism \(X\to Y\oplus Z\) and let \((h^1,h^2)\) for morphisms \(h^1:Y\to X\), \(h^2:Z\to X\) refer to the induced morphism \(Y\oplus Z\to X\). Let $$k:A\to A\oplus B,\;l:B\to A\oplus B,\;p:A\oplus B\to A,\;q:A\oplus B\to B$$ be the canonical morphisms.

The diagram is a cartesian square iff the following sequence is exact:$$0\to W\xrightarrow{(i,j)}A\oplus B\xrightarrow{(f,-g)}C$$The diagram is a cocartesian square if the following sequence is exact:$$W\xrightarrow{(i,-j)}A\oplus B\xrightarrow{(f,g)}C\to0$$


Let \(k:K\to A\oplus B\) be the kernel map of \((f,-g)\). By the abelian category characterization of fibered products in Abelian Categories, the diagram is a cartesian square iff there exists an isomorphism \(\phi:K\to W\) with \(i\circ\phi=p\circ k\) and \(j\circ\phi=q\circ k\). The given sequence is exact iff there exists an isomorphism \(\phi:K\to W\) with \((i,j)\circ\phi=k\). But, \(i\circ\phi=p\circ k\) and \(j\circ\phi=q\circ k\) iff $$p\circ(i,j)\circ\phi=p\circ k,\;q\circ(i,j)\circ\phi=q\circ k$$iff \((i,j)\circ\phi=k\) since \(p,q\) are epic. The other part of the lemma follows from duality.

Observe that via the cartesian square, we can induce maps \(j_*:\ker i\to\ker g\) and \(f_*:\cok i\to\cok g\) as follows: Since $$0=f\circ i\circ\ker i=g\circ j\circ\ker i$$there exists a unique morphism \(j_*\) such that \(\ker g\circ j_*=j\circ\ker i\). Likewise, since $$0=\cok g\circ g\circ j=\cok g\circ f\circ i$$there exists a unique map \(f_*\) such that \(\cok g\circ f=f_*\circ\cok i\).

If the square is cartesian, then \(j_*\) is an isomorphism. If it is cocartesian, \(f_*\) is.


Observe that $$g\circ\ker g=f\circ0=0$$so by the cartesian property, there exists a map \(\eta:\ker g\to W\) such that $$i\circ\eta=0,\;j\circ\eta=\ker g$$By kernel properties, there exists a unique map \(j_*^{-1}:\ker g\to\ker i\) such that \(\eta=\ker i\circ j^{-1}_*\). Since uniqueness composes, \(j_*\circ j^{-1}_*\) and \(j^{-1}_*\circ j_*\) are both unique maps that satisfy their respective relations. Since \(\id_W\) and \(\id_B\) satisfy the respective relations, we have that \(j_*\) and \(j_*^{-1}\) are inverses and thus isomorphisms. By duality, the lemma follows.
If the square is cartesian and \(g\) is epic, then \(i\) is epic and the square is also cocartesian. Dually, if the square is cocartesian and \(j\) is monic, then \(f\) is monic and the square is also cartesian.


Assuming \(g\) is epic, \((g,-f):A\oplus B\to C\) is epic. Thus, by Lemma 1, the following sequence is exact:$$0\to W\xrightarrow{(i,j)} A\oplus B\xrightarrow{(g,-f)}C\to0$$Thus, the square is cocartesian by Lemma 1. And, by Lemma 2, we know that \(\cok i\to\cok g\) is an isomorphism, and with \(\cok g\cong0\) (as \(g\) is epic), \(i\) must be epic as well since \(\cok i\cong0\). The remainder of the lemma is true by duality.
The sequence $$A\xrightarrow fB\xrightarrow gC$$is exact iff for every \(h:X\to B\) with \(g\circ h=0\), there exists an object \(Y\), an epimorphism \(e:Y\to X\), and a morphism \(k:Y\to A\) with \(h\circ e=f\circ k\).


Let \(j:\im f\to\ker g\) be the monomorphism derived in (Co)homology and Exactness. Let \(i\) be the kernel map \(\ker g\to B\). Let \(p:A\to\im f\) be the standard epimorphism from Lemma \(4\) in Abelian Categories.
  • \((\Longrightarrow)\): Let \(h:X\to B\) satisfy \(g\circ h=0\). By kernel properties, there exists a map \(\alpha:X\to\ker g\) such that \(i\circ\alpha=h\). Likewise, since \(g\circ f=0\), there exists a map \(\beta:A\to\ker g\) such that \(f=i\circ\beta\). Thus, we can define \(P=A\times_{\ker g}X\), with projection maps \(k:P\to A,\;e:P\to X\). This implies that \(\alpha\circ e=\beta\circ k\), so $$h\circ e=f\circ k=i\circ j\circ p\circ k$$(since \(f=i\circ j\circ p\) from Lemma 4 in Abelian Categories. \(j\circ p\) is trivially epic, and the above equality implies that \(\beta=j\circ p\), so by Lemma 3, \(e\) is also epic.

  • \((\Longleftarrow)\): \(g\circ i=0\) by kernel properties, so by assumption, there exists epimorphism \(e:Y\to\ker g\) and morphism \(k:Y\to A\) such that \(i\circ e=f\circ k\). So, $$i\circ e=i\circ j\circ p\circ k$$Since \(i\) is monic, \(e=j\circ p\circ k\). So, \(j\) must be an epimorphism, and thus must be an isomorphism by Lemma 2 in Abelian Categories. This obviously implies that the sequence is exact.
Given the following commutative diagram, if the first row is exact and \(k\) monic, the induced sequence (see the paragraph before Lemma 2 for an explicit induction) $$\ker a\xrightarrow d\ker b\xrightarrow e\ker c$$ is exact. Dually, if the second row is exact and \(g\) is epic, \(\cok a\to\cok b\to\cok c\) is exact.


Suppose the first row is exact and \(k\) is monic. Let $$h:\ker a\to X,\;i:\ker b\to Y,\;j:\ker c\to Z$$ be kernel morphisms. By construction, the following diagram commutes:

Note that $$j\circ e\circ d=g\circ f\circ h=0$$since \(j\) is monic, \(e\circ d=0\). For any map \(s:B\to\ker b\) such that \(e\circ s=0\), \(j\circ e\circ s=g\circ i\circ s\), so by Lemma 4 applied to the map \(i\circ s\), there exists an object \(P\), epimorphism \(\alpha:P\to B\), morphism \(\beta:P\to X\) such that \(f\circ\beta=i\circ s\circ\alpha\). So, $$k\circ a\circ\beta =b\circ f\circ\beta=b\circ i\circ s\circ\alpha=0$$\(k\) is monic, so \(a\circ\beta=0\). So, there is a unique morphism \(m:P\to\ker a\) with \(\beta=h\circ m\). So, $$i\circ s\circ\alpha=f\circ\beta=f\circ h\circ m=i\circ d\circ m$$Since \(i\) is monic, \(s\circ\alpha=d\circ m\).

By Lemma 4, \(\ker a\to\ker b\to\ker c\) is exact. By duality, the rest follows.
Consider the following chain morphism of exact sequences:

There exists a unique morphism \(\partial:\ker c\to\cok a\) that satisfies the commutative diagram

And the following sequence is exact:$$\ker a\xrightarrow{f^*}\ker b\xrightarrow{g^*}\ker c\xrightarrow\partial\cok a\xrightarrow{k^*}\cok b\xrightarrow{l^*}\cok c$$with \(f^*\) monic if \(f\) is, and \(l^*\) epic if \(l\) is.


For notational simplicity, let \(P=Y\times_Z\ker c\), \(Q=\cok a\:\sqcup_U\:V\). Lemma 3 implies that \(\beta\) is epic and \(i\) is monic, so uniqueness of \(\partial\) is given. Since \(\beta\) is epic, we can extend it into a short exact sequence as done in (Co)homology and Exactness, and similarly for \(i\), we can extend into a short exact sequence. Let \(h:\ker b\to Y\) be a kernel morphism (not on the diagram). Thus, the following diagram has exact rows:

Since $$l\circ b\circ a=c\circ k\circ\beta=0$$and the third row of the diagram is exact, by Lemma 4 applied to \(b\circ a\), we have a morphism \(\phi:P\to U\) with \(k\circ\phi=b\circ\alpha\). By Lemma 2, since the upper right square is cartesian, \(\ker\beta\cong\ker g\), so by kernel properties of \(g\), there exists a unique map \(\pi:X\to\ker\beta\) such that \(\alpha\circ p\circ\pi=f\). Since \(\ker\beta\) is a kernel of \(g\), it can also be viewed as the image of \(f\) since the sequence is exact. Thus, \(\pi\) is the canonical map \(X\to\im f\), and thus must be epic.

Thus, $$k\circ\phi\circ p\circ\pi=b\circ\alpha\circ p\circ\pi=b\circ f=k\circ a$$\(k\) is monic and \(\pi\) is epic, so \(c\circ\phi\circ p=0\). By the cokernel properties of \(\beta\), there exists a morphism \(\partial:\ker c\to\cok a\) such that \(\partial\circ\beta=c\circ\phi\). We have now constructed the snake morphism. It trivially satisfies the commutative diagram, and thus, the first part of the proof is complete.

To now show that the sequence is exact, consider some morphism \(\psi: R\to\ker c\) such that \(\partial\circ\psi=0\). By Lemma 4 applied to \(\psi\) on the exact sequence \(P\xrightarrow\beta\ker c\to0\), we get an object \(S\), a morphism \(\eta:S\to P\), and an epimorphism \(\zeta:S\to R\) such that \(\psi\circ\zeta=\beta\circ\eta\). Since $$c\circ\phi\circ\eta=\partial\circ\psi\circ\zeta=0$$we again apply Lemma 4 to the exact sequence \(X\to U\to\cok a\) to get an object \(T\), epimorphism \(\varepsilon: T\to S\), morphism \(\gamma: T\to X\) such that $$\phi\circ\eta\circ\varepsilon=a\circ\gamma$$So, $$b\circ f\circ\gamma=k\circ a\circ\gamma=k\circ\phi\circ\eta\circ\varepsilon=b\circ\alpha\circ\eta\circ\varepsilon$$Thus, letting \(\Delta=\alpha\circ\eta\circ\varepsilon-f\circ\gamma\), \(b\circ\Delta=0\). By kernel properties, there exists a unique morphism \(\chi:T\to\ker b\) such that \(q\circ\chi=\Delta\).

To now show that the sequence is exact, consider some morphism \(\psi: R\to\ker c\) such that \(\partial\circ\psi=0\). By Lemma 4 applied to \(\psi\) on the exact sequence \(P\xrightarrow\beta\ker c\to0\), we get an object \(S\), a morphism \(\eta:S\to P\), and an epimorphism \(\zeta:S\to R\) such that \(\psi\circ\zeta=\beta\circ\eta\). Since $$c\circ\phi\circ\eta=\partial\circ\psi\circ\zeta=0$$we again apply Lemma 4 to the exact sequence \(X\to U\to\cok a\) to get an object \(T\), epimorphism \(\varepsilon: T\to S\), morphism \(\gamma: T\to X\) such that $$\phi\circ\eta\circ\varepsilon=a\circ\gamma$$So, $$b\circ f\circ\gamma=k\circ a\circ\gamma=k\circ\phi\circ\eta\circ\varepsilon=b\circ\alpha\circ\eta\circ\varepsilon$$Thus, letting \(\Delta=\alpha\circ\eta\circ\varepsilon-f\circ\gamma\), \(b\circ\Delta=0\). By kernel properties, there exists a unique morphism \(\chi:T\to\ker b\) such that \(q\circ\chi=\Delta\).

This proof is a classic example of an "abstract nonsense" proof. For basically every other proof we've done, the intuition behind the steps taken was pretty clear as we took them, but here, a lot of steps feel contrived. In my opinion, the best way to think about this lemma is that the boundary map, \(\partial\), can be "defined" as \(k^{-1}\circ b\circ g^{-1}\), since \(g\) is epic (and thus right-invertible in nice categories) and \(k\) is monic (and thus left-invertible in nice categories). Obviously, this is a big handwave, but it should provide a bit more context for the lemma.

Abelianizing infinite chain complexes

Infinite chain complexes are very useful, since they inherit a lot of the structure of the underlying category. In fact, we can define a category of cochain complexes as follows (one can do this for chain complexes as well). Let \(\rmC\) be an abelian category. We define the category \(Com_\rmC\) as follows. The elements are infinite cochain complexes $$A^*:\qquad\ldots\to A^{i-1}\xrightarrow{f^{i-1}}A^i\xrightarrow{f^i}A^{i+1}\to\ldots$$of objects in \(\rmC\), and morphisms \(A^*\to B^*\) are morphisms \(m_i:A^i\to B^i\) satisfying the diagram

\(Com_\rmC\) is abelian.


This is a proof sketch, as the proof is trivial but tedious. Defining the zero-object as the \(0\) chain complex, and defining morphism addition, composition, chain complex products, kernels, cokernels pointwise imposes an abelian structure on \(Com_\rmC\).

(Co)homology Morphisms

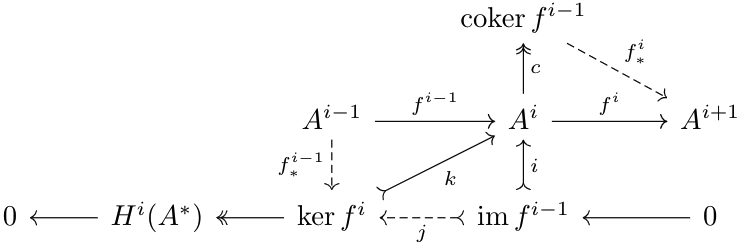
A morphism \(m:A^*\to B^*\) induces a homology map \(H^i(A^*)\to H^i(B^*)\), and thus creates a functor \(H^i:Com_\rmC\mapsto\rmC\).


From the (Co)homology and Exactness post, we used the following diagram to generate the short exact sequence defining the homology.

Imagine a similar diagram with \(f\)s replaced with \(g\)s and \(A\)s replaced with \(B\)s for \(B^*\). We combine these two diagrams with the \(m_i\) morphisms presented in the definition of chain complex morphisms.

Observe that $$0=m_{i+1}\circ f_i\circ k_A=g_i\circ m_i\circ k_A$$so by the kernel properties of \(k_B\), there exists a unique map \(K:\ker f^i\to\ker g^i\) such that \(m_i\circ k_A=k_B\circ K\). Likewise, since $$0=c_B\circ g^{i-1}\circ m_{i-1}= c_B\circ m_i\circ f^{i-1}$$there exists a unique map \(C:\cok f^{i-1}\to\cok g^{i-1}\) such that \(c_B\circ m_i=C\circ c_A\). Thus, $$0=C\circ c_A\circ i_A=c_B\circ m_i\circ i_A$$Thus, by the kernel properties of \(i_B\), there exists a unique map \(I:\im f^{i-1}\to\im g^{i-1}\) such that \(m_i\circ i_A=i_B\circ I\).

Since \(K,I,j_A,j_B\) are all unique morphisms which satisfy their relations, and since uniqueness is preserved under composition, \(K\circ j_A\) and \(j_B\circ I\) are both unique morphisms satisfying their relations. However, they both are maps \(\im f^{i-1}\to\ker g^i\). Thus, \(K\circ j_A=j_B\circ I\).

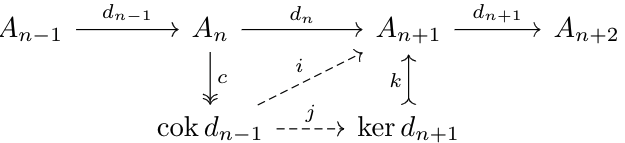
Let \(x_A:\ker f^i\to H^i(A^*)\) be the cokernel of \(j_A\), and define \(x_B\) similarly. So, $$0=x_B\circ j_B\circ I=x_B\circ K\circ j_A$$Thus, by the cokernel property of \(x_A\), there exists a unique map \(H:H^i(A^*)\to H^i(B^*)\) such that \(x_B\circ K=H\circ x_A\). We define the functor \(H^i\) as the functor that sends \(m\to H\). By construction, it is a covariant functor.
Given a short exact sequence in \(Com_\rmC\) (\(X^*\) is the cochain complex $$X_i\xrightarrow{d^X_i}X_{i+1}\xrightarrow{d^X_{i+1}}\ldots$$and \(h:X^*\to Y^*\) are morphisms \(h^i:X_i\to Y_i\) satisfying the natural commutative diagram)$$0\to A^*\xrightarrow fB^*\xrightarrow gC^*\to0$$There exists a long exact sequence of cohomology (dually, homology)


Consider the following subsequence of \(A^*\) (\(d^n\) refers to \(d^A_n\)):

Observe that there exists a unique morphism \(i:\cok d_{n-1}^A\to A_{n+1}\) satisfying \(i\circ c=d_n^A\) by the cokernel properties of \(c\). Thus, $$0=d_{n+1}^A\circ d_n^A=d_{n+1}^A\circ i\circ c$$Since \(c\) is epic, \(d_{n+1}^A\circ i=0\), and thus, by the kernel properties of \(k\), there exists a unique morphism \(j:\cok d_{n-1}^A\to\ker d_{n+1}^A\) such that \(k\circ j=i\).

Now consider \(\im d_n^A\). We know that there's a monomorphism \(q:\im d_n^A\to\ker d_{n+1}^A\) and an epimorphism \(h:A_n\to\im d_n^A\) that commute with the diagram above. Thus, $$0=d_n^A\circ d_{n-1}^A=k\circ q\circ h\circ d_{n-1}^A$$Since \(k\circ q\) is monic, \(h\circ d_{n-1}^A=0\). Thus, by cokernel properties, there exists a unique morphism \(r:\cok d_{n-1}^A\to\im d_n^A\) such that \(q\circ r=j\). This map, therefore, is a map \(\cok d_{n-1}^A\to\coim d_n^A\) since \(\im d_n^A\) is also the coimage of \(d_n^A\) (Lemma \(4\) of Abelian Categories)

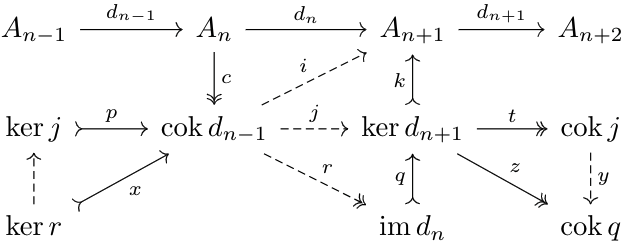
I claim that \(\ker j\) is a kernel for \(r\). For any kernel \(x:\ker r\to\cok d_{n-1}^A\) with \(r\circ x=0\), $$j\circ x=q\circ r\circ x=0$$so there exists a morphism \(\tau:\ker r\to\ker j\) with \(p\circ \tau=x\). This implies that \(\ker j\) is a kernel for \(r\). In particular, we have by a result in (Co)homology and Exactness$$\ker j=\ker(\cok d_{n-1}^A\to \coim d_n^A)=H^n(A^*)$$Next, observe that since \(r\circ c=h\), and \(h\) is epimorphic, \(r\) must also be epimorphic.

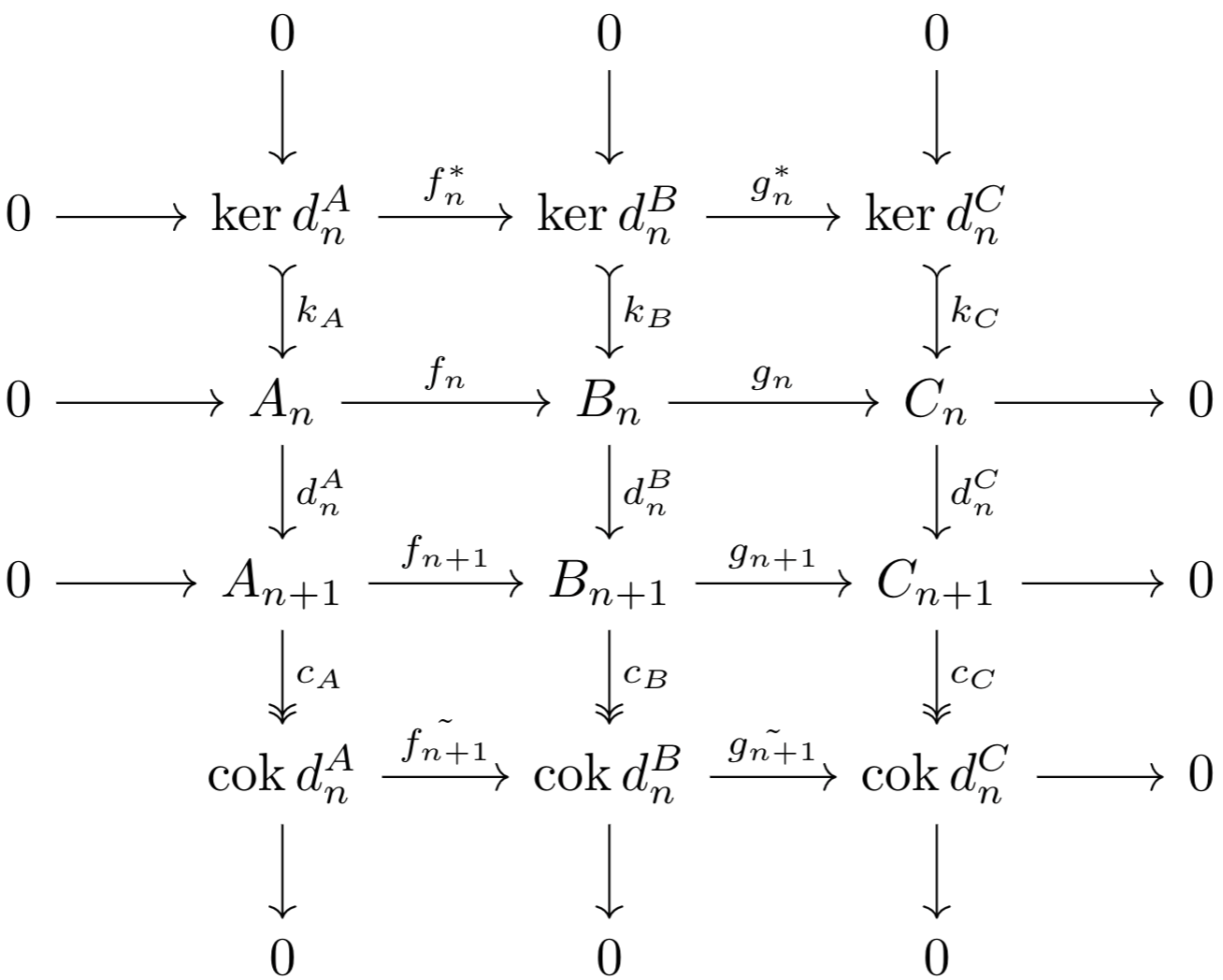
We want to show that \(\cok j\) is a cokernel for \(q\). Note that $$0=t\circ j=t\circ q\circ r$$Since \(r\) is epic, \(t\circ q=0\). And, given \(z:\ker d_{n+1}^A\to\cok q\) a cokernel for \(q\), \(z\circ q=0\), so $$z\circ j=z\circ q\circ r=0$$thus, there exists a map \(y:\cok j\to\cok q\) such that \(y\circ t=z\). This implies that \(\cok j\) is a cokernel for \(q\). So, $$\cok j=\cok(\im d_n^A\to\ker d_{n+1}^A)=H^{n+1}(A^*)$$Next, I claim that the following diagram commutes and has exact rows and columns:

First, let's begin with the columns. \(\im k_A=k_A\), and \(\ker d_n^A=k_A\). $$\ker c_A=\ker(\cok(d_n^A))=\im d_n^A$$This completes the proof of the columns being exact. Moreover, the middle two rows are exact and commute by definition of a chain morphism. Next, let's generate the morphisms $$f^*_n,g^*_n,\tilde{f_{n+1}},\tilde{g_{n+1}}$$

Since $$0=f_{n+1}\circ d_n^A\circ k_A=d_n^B\circ f_n\circ k_A$$there exists a map \(f^*_n:\ker d_n^A\to\ker d_n^B\) such that \(f_n\circ k_A=k_B\circ f^*_n\). The same logic will generate \(g^*_n\). Since \(k_B\), \(f_n\circ k_A\) are monic, so is \(f^*_n\). Thus, \(\im f^*_n=f^*_n\). For any morphism \(x: K\to \ker d_n^B\) such that \(g^*_n\circ x=0\), $$0=k_C\circ g^*_n\circ x=g_n\circ k_B\circ x$$so by kernel properties, there exists a unique map \(\phi:K\to A_n\) such that \(f_n\circ\phi=k_B\circ x\). Thus, $$f_{n+1}\circ d_n^A\circ\phi=d_n^B\circ f_n\circ\phi=d_n^B\circ k_B\circ x=0$$Since \(f_{n+1}\) is monic, \(d_n^A\circ\phi=0\), so there exists a unique map \(\psi:K\to\ker d_n^A\) such that \(f^*_n\circ\psi=\phi\). This implies that \(f^*_n=\ker g^*_n\), and thus, the upper row is exact and commutes with the middle rows.

The dual arguments will construct \(\tilde{f_{n+1}},\;\tilde{g_{n+1}}\), show that they commute with the middle rows (and thus with the diagram), and show that \(\tilde{g_{n+1}}\) is the cokernel of \(\tilde{f_{n+1}}\). With this, we can construct the following chain morphism of exact sequences (the rows are exact and the diagram commutes thanks to the results above) for any \(n\).

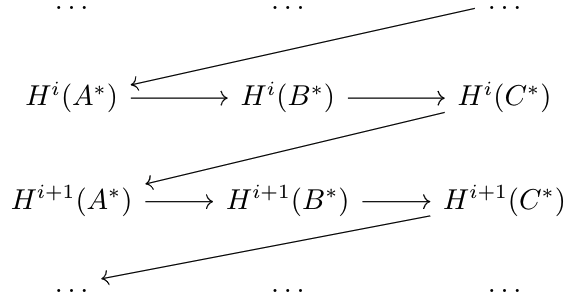
By Theorem 3, we have an exact sequence $$H^n(A^*)\to H^n(B^*)\to H^n(C^*)\to H^{n+1}(A^*)\to H^{n+1}(B^*)\to H^{n+1}(C^*)$$Since we can construct this sequence for any \(n\), we can string them all together to form our long exact cohomology sequence. Dually, we can do the same for an exact sequence of chain complexes and a long exact sequence of homology.
This is one of the most important results for the subject that can be proved purely categorically. As a quick example, the Mayer-Vietoris sequence can be shown via this theorem.
Top