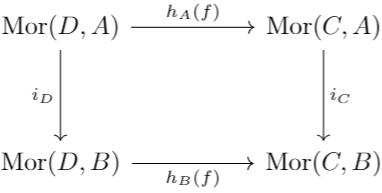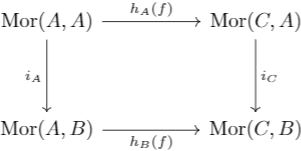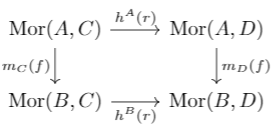\ie \cf

$\newcommand{\rank}{\text{rank}} \newcommand{\tr}{\text{tr}} \newcommand{\mor}{\text{Mor}} \newcommand{\hom}{\text{Hom}} \newcommand{\id}{\text{id}} \newcommand{\obj}{\text{obj}} \newcommand{\pr}{\text{pr}} \newcommand{\ker}{\text{ker}} \newcommand{\coker}{\text{coker}} \newcommand{\im}{\text{im}} \newcommand{\vol}{\text{vol}} \newcommand{\disc}{\text{disc}} \newcommand{\bbA}{\mathbb A} \newcommand{\bbB}{\mathbb B} \newcommand{\bbC}{\mathbb C} \newcommand{\bbD}{\mathbb D} \newcommand{\bbE}{\mathbb E} \newcommand{\bbF}{\mathbb F} \newcommand{\bbG}{\mathbb G} \newcommand{\bbH}{\mathbb H} \newcommand{\bbI}{\mathbb I} \newcommand{\bbJ}{\mathbb J} \newcommand{\bbK}{\mathbb K} \newcommand{\bbL}{\mathbb L} \newcommand{\bbM}{\mathbb M} \newcommand{\bbN}{\mathbb N} \newcommand{\bbO}{\mathbb O} \newcommand{\bbP}{\mathbb P} \newcommand{\bbQ}{\mathbb Q} \newcommand{\bbR}{\mathbb R} \newcommand{\bbS}{\mathbb S} \newcommand{\bbT}{\mathbb T} \newcommand{\bbU}{\mathbb U} \newcommand{\bbV}{\mathbb V} \newcommand{\bbW}{\mathbb W} \newcommand{\bbX}{\mathbb X} \newcommand{\bbY}{\mathbb Y} \newcommand{\bbZ}{\mathbb Z} \newcommand{\cA}{\mathcal A} \newcommand{\cB}{\mathcal B} \newcommand{\cC}{\mathcal C} \newcommand{\cD}{\mathcal D} \newcommand{\cE}{\mathcal E} \newcommand{\cF}{\mathcal F} \newcommand{\cG}{\mathcal G} \newcommand{\cH}{\mathcal H} \newcommand{\cI}{\mathcal I} \newcommand{\cJ}{\mathcal J} \newcommand{\cK}{\mathcal K} \newcommand{\cL}{\mathcal L} \newcommand{\cM}{\mathcal M} \newcommand{\cN}{\mathcal N} \newcommand{\cO}{\mathcal O} \newcommand{\cP}{\mathcal P} \newcommand{\cQ}{\mathcal Q} \newcommand{\cR}{\mathcal R} \newcommand{\cS}{\mathcal S} \newcommand{\cT}{\mathcal T} \newcommand{\cU}{\mathcal U} \newcommand{\cV}{\mathcal V} \newcommand{\cW}{\mathcal W} \newcommand{\cX}{\mathcal X} \newcommand{\cY}{\mathcal Y} \newcommand{\cZ}{\mathcal Z} \newcommand{\rmA}{\mathfrak A} \newcommand{\rmB}{\mathfrak B} \newcommand{\rmC}{\mathfrak C} \newcommand{\rmD}{\mathfrak D} \newcommand{\rmE}{\mathfrak E} \newcommand{\rmF}{\mathfrak F} \newcommand{\rmG}{\mathfrak G} \newcommand{\rmH}{\mathfrak H} \newcommand{\rmI}{\mathfrak I} \newcommand{\rmJ}{\mathfrak J} \newcommand{\rmK}{\mathfrak K} \newcommand{\rmL}{\mathfrak L} \newcommand{\rmM}{\mathfrak M} \newcommand{\rmN}{\mathfrak N} \newcommand{\rmO}{\mathfrak O} \newcommand{\rmP}{\mathfrak P} \newcommand{\rmQ}{\mathfrak Q} \newcommand{\rmR}{\mathfrak R} \newcommand{\rmS}{\mathfrak S} \newcommand{\rmT}{\mathfrak T} \newcommand{\rmU}{\mathfrak U} \newcommand{\rmV}{\mathfrak V} \newcommand{\rmW}{\mathfrak W} \newcommand{\rmX}{\mathfrak X} \newcommand{\rmY}{\mathfrak Y} \newcommand{\rmZ}{\mathfrak Z} \newcommand{\paren}[1]{( #1 )} \newcommand{\Paren}[1]{\left( #1 \right)} \newcommand{\bigparen}[1]{\bigl( #1 \bigr)} \newcommand{\Bigparen}[1]{\Bigl( #1 \Bigr)} \newcommand{\biggparen}[1]{\biggl( #1 \biggr)} \newcommand{\Biggparen}[1]{\Biggl( #1 \Biggr)} \newcommand{\abs}[1]{\lvert #1 \rvert} \newcommand{\Abs}[1]{\left\lvert #1 \right\rvert} \newcommand{\bigabs}[1]{\bigl\lvert #1 \bigr\rvert} \newcommand{\Bigabs}[1]{\Bigl\lvert #1 \Bigr\rvert} \newcommand{\biggabs}[1]{\biggl\lvert #1 \biggr\rvert} \newcommand{\Biggabs}[1]{\Biggl\lvert #1 \Biggr\rvert} \newcommand{\card}[1]{\left| #1 \right|} \newcommand{\Card}[1]{\left\lvert #1 \right\rvert} \newcommand{\bigcard}[1]{\bigl\lvert #1 \bigr\rvert} \newcommand{\Bigcard}[1]{\Bigl\lvert #1 \Bigr\rvert} \newcommand{\biggcard}[1]{\biggl\lvert #1 \biggr\rvert} \newcommand{\Biggcard}[1]{\Biggl\lvert #1 \Biggr\rvert} \newcommand{\norm}[1]{\lVert #1 \rVert} \newcommand{\Norm}[1]{\left\lVert #1 \right\rVert} \newcommand{\bignorm}[1]{\bigl\lVert #1 \bigr\rVert} \newcommand{\Bignorm}[1]{\Bigl\lVert #1 \Bigr\rVert} \newcommand{\biggnorm}[1]{\biggl\lVert #1 \biggr\rVert} \newcommand{\Biggnorm}[1]{\Biggl\lVert #1 \Biggr\rVert} \newcommand{\iprod}[1]{\langle #1 \rangle} \newcommand{\Iprod}[1]{\left\langle #1 \right\rangle} \newcommand{\bigiprod}[1]{\bigl\langle #1 \bigr\rangle} \newcommand{\Bigiprod}[1]{\Bigl\langle #1 \Bigr\rangle} \newcommand{\biggiprod}[1]{\biggl\langle #1 \biggr\rangle} \newcommand{\Biggiprod}[1]{\Biggl\langle #1 \Biggr\rangle} \newcommand{\set}[1]{\lbrace #1 \rbrace} \newcommand{\Set}[1]{\left\lbrace #1 \right\rbrace} \newcommand{\bigset}[1]{\bigl\lbrace #1 \bigr\rbrace} \newcommand{\Bigset}[1]{\Bigl\lbrace #1 \Bigr\rbrace} \newcommand{\biggset}[1]{\biggl\lbrace #1 \biggr\rbrace} \newcommand{\Biggset}[1]{\Biggl\lbrace #1 \Biggr\rbrace} \newcommand{\bracket}[1]{\lbrack #1 \rbrack} \newcommand{\Bracket}[1]{\left\lbrack #1 \right\rbrack} \newcommand{\bigbracket}[1]{\bigl\lbrack #1 \bigr\rbrack} \newcommand{\Bigbracket}[1]{\Bigl\lbrack #1 \Bigr\rbrack} \newcommand{\biggbracket}[1]{\biggl\lbrack #1 \biggr\rbrack} \newcommand{\Biggbracket}[1]{\Biggl\lbrack #1 \Biggr\rbrack} \newcommand{\ucorner}[1]{\ulcorner #1 \urcorner} \newcommand{\Ucorner}[1]{\left\ulcorner #1 \right\urcorner} \newcommand{\bigucorner}[1]{\bigl\ulcorner #1 \bigr\urcorner} \newcommand{\Bigucorner}[1]{\Bigl\ulcorner #1 \Bigr\urcorner} \newcommand{\biggucorner}[1]{\biggl\ulcorner #1 \biggr\urcorner} \newcommand{\Biggucorner}[1]{\Biggl\ulcorner #1 \Biggr\urcorner} \newcommand{\ceil}[1]{\lceil #1 \rceil} \newcommand{\Ceil}[1]{\left\lceil #1 \right\rceil} \newcommand{\bigceil}[1]{\bigl\lceil #1 \bigr\rceil} \newcommand{\Bigceil}[1]{\Bigl\lceil #1 \Bigr\rceil} \newcommand{\biggceil}[1]{\biggl\lceil #1 \biggr\rceil} \newcommand{\Biggceil}[1]{\Biggl\lceil #1 \Biggr\rceil} \newcommand{\floor}[1]{\lfloor #1 \rfloor} \newcommand{\Floor}[1]{\left\lfloor #1 \right\rfloor} \newcommand{\bigfloor}[1]{\bigl\lfloor #1 \bigr\rfloor} \newcommand{\Bigfloor}[1]{\Bigl\lfloor #1 \Bigr\rfloor} \newcommand{\biggfloor}[1]{\biggl\lfloor #1 \biggr\rfloor} \newcommand{\Biggfloor}[1]{\Biggl\lfloor #1 \Biggr\rfloor} \newcommand{\lcorner}[1]{\llcorner #1 \lrcorner} \newcommand{\Lcorner}[1]{\left\llcorner #1 \right\lrcorner} \newcommand{\biglcorner}[1]{\bigl\llcorner #1 \bigr\lrcorner} \newcommand{\Biglcorner}[1]{\Bigl\llcorner #1 \Bigr\lrcorner} \newcommand{\bigglcorner}[1]{\biggl\llcorner #1 \biggr\lrcorner} \newcommand{\Bigglcorner}[1]{\Biggl\llcorner #1 \Biggr\lrcorner} \newcommand{\Rnn}{\R_{\ge 0}} \DeclareMathOperator{\Tr}{Tr} \DeclareMathOperator{\Inf}{Inf} \DeclareMathOperator{\min}{min} \DeclareMathOperator{\max}{max} \DeclareMathOperator{\argmax}{arg\,max} \DeclareMathOperator{\argmin}{arg\,min} \DeclareMathOperator{\E}{\mathbb E} \DeclareMathOperator{\pE}{\tilde{\mathbb E}} \DeclareMathOperator{\Pr}{\mathbb P} \DeclareMathOperator{\Det}{\textbf{Det}} \DeclareMathOperator{\Perm}{\textbf{Perm}} \DeclareMathOperator{\Sym}{\textbf{Sym}} \DeclareMathOperator{\Pow}{\textbf{Pow}} \DeclareMathOperator{\Gal}{\textbf{Gal}} \DeclareMathOperator{\Aut}{\textbf{Aut}} \notag$

$\newcommand{\1}{\ensuremath{\mathrm{1}}} \notag$

$\newcommand{\transpose}[1]{\ensuremath{#1{}^{\mkern-2mu\intercal}}} \newcommand{\nchoose}[1]{\ensuremath} \newcommand{\generated}[1]{\ensuremath{\langle #1 \rangle}} \notag$

\newcommand{\eqdef}{\mathbin{\stackrel{\rm def}{=}}}  \newcommand{\R} % real numbers  \newcommand{\N}} % natural numbers  \newcommand{\Z} % integers  \newcommand{\F} % a field  \newcommand{\Q} % the rationals  \newcommand{\C}{\mathbb{C}} % the complexes  \newcommand{\poly}}  \newcommand{\polylog}}  \newcommand{\loglog}}}  \newcommand{\zo}{\{0,1\}}  \newcommand{\suchthat}  \newcommand{\pr}[1]{\Pr\left[#1\right]}  \newcommand{\deffont}{\em}  \newcommand{\getsr}{\mathbin{\stackrel{\mbox{\tiny R}}{\gets}}}  \newcommand{\Exp}{\mathop{\mathrm E}\displaylimits} % expectation  \newcommand{\Var}{\mathop{\mathrm Var}\displaylimits} % variance  \newcommand{\xor}{\oplus}  \newcommand{\GF}{\mathrm{GF}}  \newcommand{\eps}{\varepsilon}  \notag

$\newcommand{\pr}[1]{\Pr\left[#1\right]} \notag$

$\newcommand{\MIP}{\class{MIP}}$

\no

$\newcommand{\textprob}[1]{\text{#1}} \newcommand{\mathprob}[1]{\textbf{#1}} \newcommand{\Satisfiability}{\textprob{Satisfiability}} \newcommand{\Mor}{\textprob{Mor}} \newcommand{\Hom}{\textprob{Hom}} \newcommand{\cok}{\textprob{cok}} \newcommand{\ker}{\textprob{ker}} \newcommand{\im}{\textprob{im}} \newcommand{\coim}{\textprob{coim}} \newcommand{\id}{\textprob{id}}$

Next |

| Previous

Yoneda Lemma

100%

Before we move on to the more involved structures in Category Theory, it's worth taking a detour through proving Yoneda's lemma. Roughly speaking, Yoneda's lemma tells us that the information of an object is completely described by its functor of points.

Let $h_A$ be the functor of points for object $A$. Thus, for any $f:C\to D\in\mathfrak C$, $h_A(f):\Mor(D,A)\to\Mor(C,A)$.

Suppose that for two objects $A,B\in\mathfrak C$, there are morphisms $i_C:\Mor(C,A)\to\Mor(C,B)$ for every $C\in\mathfrak C$ that commute with the morphisms $h_A(f)$ as defined earlier in the natural way (see diagram below). Thus, there exists $g:A\to B$ such that $i_C:u\mapsto g\circ u$ for all $C\in\mathfrak C$. If $i_C$ is a bijection for all $C$, then $g$ is an isomorphism.

Let $g=i_A(\id)$. Thus, letting $D=A$, we transform the diagram to

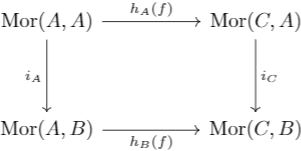
If we consider the morphism $\id\in\Mor(A,A)$, the diagram tells us that $i_C(f)=g\circ f$. If $i_B$ is a bijection, there exists some $f:B\to A$ such that $i_B(f)=\id$. Thus, $g\circ f=\id$, and this shows that $g$ is an isomorphism.

This lemma also holds with the arrows in the diagrams above flipped, and with the functor of points replaced with $\Mor(C,-)$. We'll call this covariant functor $h^C$.

There exists a natural bijection between the collection of natural transformations $h^A\to h^B$ and $\Mor(B,A)$.

A natural transformation $h^A\to h^B$ needs to assign to each $C\in\rmC$ a morphism $m_C:h^A(C)\to h^B(C) = \Mor(A,C)\to\Mor(B,C)$. Clearly, for any $f\in\Mor(B,A)$, we can let $m_C=h_C(f)$, as the commutative diagram for natural transformations is satisfied below for any $r:C\to D\in\rmC$.

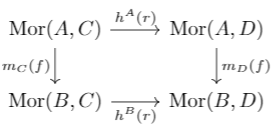
This gives us an injection from $\Mor(B,A)$ to the collection of natural transformations. Lemma 1 gives us an injection in the reverse direction.

We can write a similar lemma about natural transformations between $h_A\to h_B$ and $\Mor(A,B)$.

We call any contravariant functor $F:\rmC\to\textbf{Set}$, representable iff there exists a natural isomorphism $\epsilon:F\to h_A$ for some $A\in\mathfrak C$. We call $A$ the representing object, and it's not hard to see that it is determined up to unique isomorphism by $(F,\epsilon)$.

We call $\epsilon^{-1}(\id_A)$ the universal object of $\rmC$.

For a functor $F:\mathfrak C\to\textbf{Set}$, there exists a bijection between the collection of natural transformations $h^A\to F$ and $F(A)$. (This lemma can also be defined for contravariant functors, but the proof is a dual to this proof). This induces a natural isomorphism between the functors $\Mor(h^{(-)},F)$ and $F(-)$.

Let $\phi:h^A\to F$ be a natural transformation. For every $B\in\mathfrak C$, we have a mapping $\phi_B:\Mor(A,B)\to F(B)$ such that for any $f:X\to Y\in\mathfrak C$, the following diagram commutes:

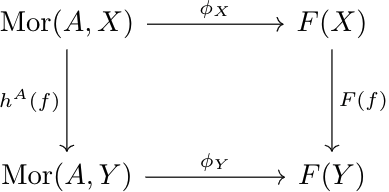
Letting $X=A$, we know that $\id\in\Mor(A,A)$. Letting $g=\phi_A(\id)$ (the universal object), the diagram tells us that for any $f:A\to Y\in\mathfrak C$, $\phi_Y(f)=F(f)(g)$.

Thus, $\phi_Y$ is fully determined by $g$, meaning that the map $\phi\mapsto g$ is an injection. Thus, we have an injection from the set of natural transformations of $h^A\to F$, and the set $F(A)$.

For the opposite direction, note that for any $x\in F(A)$, $B\in\mathfrak C$, $\phi_B:f\mapsto F(f)(x)$ is an injection. But this is the implication of the first lemma, and thus we are done.

Thus, Yoneda's lemma tells us that given a category, we can produce a category of contravariant functors from the category to Set, with morphisms as natural transformations. And, we have a functor from the original category to the new one which sends any object to its functor of points. And, this mapping is fully faithful.

Top