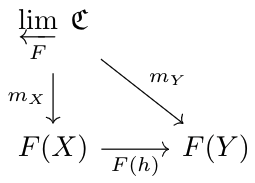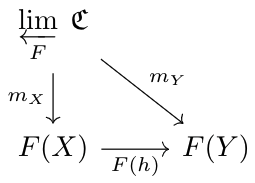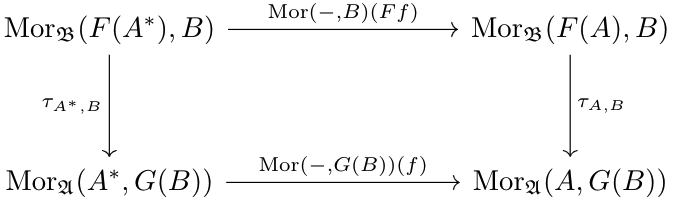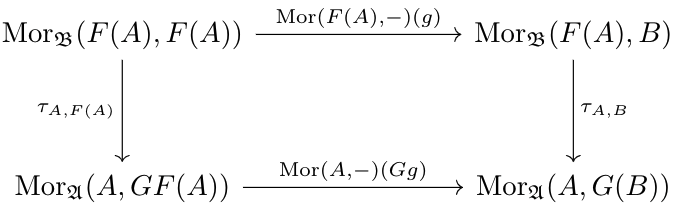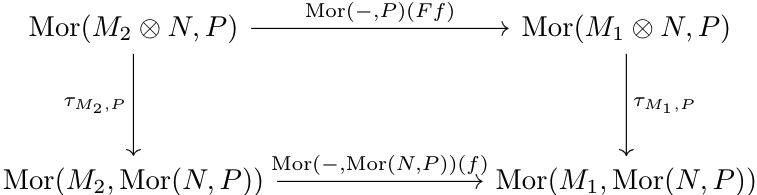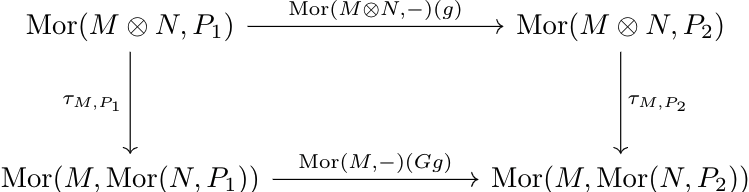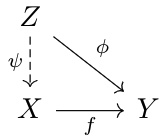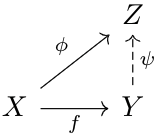Universal Properties

• Initial/Final/Zero Objects: the trivial objects in a category
• Tensor Product: a product with module structure
• Limits: in Set, products under an equivalence relation
• Colimits: in Set, disjoint unions under an equivalence relation
• Adjoints: pairs of functors that are inverses in a natural way
• (Mono/Epi)morphism: (Left/right) cancellatable morphisms

As mentioned in Why bother with Categories?, universal properties are part of the key appeal of category theory, since they are easy to express, and when done well (as we saw with the product definition), they give us uniqueness for free, leaving us to find an example of an object satisfying the property.

In this post, we'll go over some valuable universal properties. All of them are unique, but the proofs of these won't be provided since they are essentially identical to that of the product's uniqueness.

For a lot of universal properties, the intuition behind the definitions is unclear from the setup, but examples can often help show the purpose of the properties. I've provided a few examples for each property.

Initial/Final/Zero Objects

An object \(C\in\mathfrak C\) is initial if for all \(A\in\mathfrak C\), \(|\Mor(C,A)|=1\). Likewise, an object \(C\in\mathfrak C\) is final if for all \(A\in\mathfrak C\), \(|\Mor(A,C)|=1\). An object \(C\in\mathfrak C\) is called the zero object if it is both initial and final.

• \(\varnothing\) is an initial object for Set and Top. Any singleton is a final object for Set and Top.
• \(\{0\}\) unsurprisingly is a final object for Ring, the category of rings. The initial object of Ring is \(\mathbb Z\), with \(\mathbb Z\to A\) given by \(n\mapsto n\cdot 1_A\) (\(1_A\) is the multiplicative identity of \(A\)).
• In the category of Field, there is no initial nor final object, as there are no field homomorphisms between fields of different characteristics (since \(1\mapsto1\)). But, if we limit to the category of fields of a particular characteristic \(n\), \(\mathbb Z/n\mathbb Z\) (with \(\mathbb Z/0\mathbb Z\) defined to be \(\mathbb Q\).) is an initial object.
• For any commutative ring \(A\) and \(S\subset A\), we can define \(S^{-1}A\) as the initial element of the category of \(A\)-algebras that send every element of \(S\) to a unit. Observe that the initial element exists if \(S\) is a multiplicative subset of \(A\). We call \(S^{-1}A\), if it exists, the localization of \(A\) at \(S\).

Tensor Product

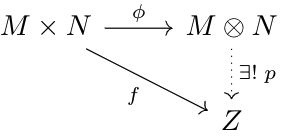
Given two elements \(M,N\in Mod_A\), we define \(M\otimes_A N\), the tensor product of \(M,N\), as the \(A\)-module, paired with an \(A\)-bilinear map \(\phi:M\times N\to M\otimes N\), that satisfies the diagram below for any \(A\)-bilinear map \(f:M\times N\to Z\), where \(Z\in Mod_A\).

• The tensor product always exists: the classical construction is as follows: let \(M\hat\times N\) be the \(A\)-module generated by symbols of the form \(m\otimes n\), where \(m\in M\), \(n\in N\), i.e., \(M\hat\times N\) consists of finite \(A\)-linear combinations of these symbols. Then, quotient \(M\hat\times N\) via the following equivalences: $$a(m\otimes n)=(am)\otimes n=m\otimes(an),\;(a+b)\otimes c=a\otimes c+b\otimes c,\;a\otimes(c+d)=a\otimes c+a\otimes d$$The result is an \(A\)-module that satisfies the universal property, and thus, is the constructive definition of the tensor product.
• \(\mathbb Z/n\mathbb Z\otimes_\mathbb Z\mathbb Z/m\mathbb Z\cong\mathbb Z/\operatorname{gcd}(n,m)\mathbb Z\). I'm not aware of a proof that solely uses the universal property definition of the tensor product rather than the constructive one for this result.
• If \(M\in Mod_A\), and \(A\to B\) is a ring morphism, we can view \(B\otimes_A M\) as a \(B\)-module, since it's an abelian group under addition, and we can define \(b\cdot(x\otimes y)=(bx)\otimes y\).
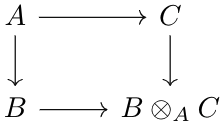
• If \(A\to B\) and \(A\to C\) are ring morphisms, \(B\otimes_A C\) can be seen as a ring, with \((b_1\otimes c_1)\cdot(b_2\otimes c_2)=(b_1b_2)\otimes(c_1c_2)\). This can be seen as a fibered coproduct (fibered products are defined later in this post, fibered coproducts are just the dual (reverse all the arrows in the diagram)) by letting \(B\to B\otimes_AC\) be defined as \(b\mapsto b\otimes1\), and \(C\to B\otimes_AC\) defined as \(c\mapsto 1\otimes c\), as the following diagram is satisfied.

  

Limits

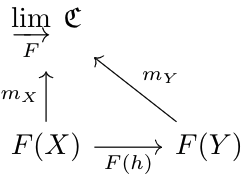
Given a small category \(\mathfrak F\), category \(\mathfrak C\), and functor \(F:\mathfrak F\to\mathfrak C\), the limit of \(\mathfrak C\) with respect to \(F\), written as \(\varprojlim\limits_F\; \mathfrak C\), is an object of \(\mathfrak C\), paired with morphisms \(m_A:\varprojlim\limits_F\; \mathfrak C\to F(A)\) for each \(A\in\mathfrak F\), such that for each morphism \(h:X\to Y\) in \(\mathfrak F\), the following diagram holds:

And such that for any other object \(W\in\mathfrak C\) with the above properties (with morphisms \(m'_A\)), there exists a map \(\phi:W\to\varprojlim\limits_F\:\mathfrak C\) such that for all \(A\in\mathfrak F\), \(m'_A=m_A\circ\phi\). In other words, \(W\)'s properties factor through the limit. (If it isn't obvious yet, this part is for uniqueness).

• If \(\mathfrak F\) is the category with two objects \(A,B\) and no morphisms between them, then \(\varprojlim\limits_F\:\mathfrak C=F(A)\times F(B)\). More generally, if \(\mathfrak F\) is some small subcategory of Id (The category of sets, with the only morphisms being the identity morphisms), we call the limit the cartesian product of the image of \(F\), i.e., $$\varprojlim\limits_F\:\mathfrak C=\prod\limits_{A\in\mathfrak F}F(A)$$
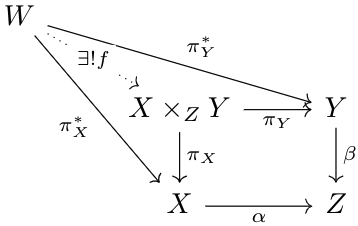
• If \(\mathfrak F\) is the following partially ordered set:

  

  Then \(\varprojlim\limits_F\:\mathfrak C\) is called the fibered product of \(A,B\) with respect to \(C\), notated as \(A\times_C B\). The fibered product (over sets) takes the cross product of fibers of \(\phi_A:A\to C\), \(\phi_B:B\to C\), and unions them, i.e., $$A\times_CB=\bigcup\limits_{c\in C}\phi_A^{-1}(c)\times\phi_B^{-1}(c)$$
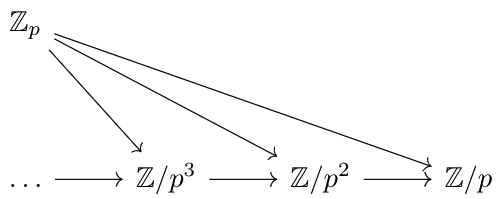
• The \(p\)-adic integers \(\mathbb Z_p\) (sometimes written as \(\mathbb Z/p^\infty\)), for a prime \(p\), is informally expressed as the ring of sums \(a_0+a_1p+a_2p^2+\ldots\), with \(0\leq p< a_i\). Observe that an arbitrary element of \(\mathbb Z/p^n\) can be expressed uniquely as \(a_0+a_1p+\ldots+a_{n-1}p^{n-1}\). Thus, there's an obvious ring morphism from \(\mathbb Z/p^m\to\mathbb Z/p^n\) (\(n\leq m\in[1,\infty]\)) given by dropping all but the first \(n\) terms. Thus, the following diagram shows how the \(p\)-adic integers can be viewed as a limit:

Colimits

Colimits, denoted by \(\varinjlim\limits_F\;\mathfrak C\), are the dual notion to limits (i.e., they satisfy the diagram with arrows reversed). More precisely, \(m_A:F(A)\to\varinjlim\limits_F\;\rmC\) is defined for each \(A\in\mathfrak F\), the diagram below holds for all \(h:X\to Y\in\mathfrak F\), and for any \(W\in\mathfrak C\) that satisfies the above properties (with \(m^*_A:F(A)\to W\) as the maps, there exists a map \(\psi:\varinjlim\limits_F\;\mathfrak C\to W\) such that \(m^*_A=\psi\circ m_A\) for each \(A\in\mathfrak F\).

• For any small category \(\mathfrak F\subset\textbf{Id}\), we notate the colimit \(\varinjlim\limits_F\;\mathfrak C\) as \(\bigsqcup\limits_{x\in\mathfrak F}F(x)\), and call it the disjoint union. If \(\mathfrak C\subset\textbf{Set}\), we can see that the disjoint union can be defined as $$\bigsqcup\limits_{x\in\mathfrak F}F(x)=\bigcup\limits_{x\in F}F(x)\times\{F(x)\}$$
• There is a nice class of small categories \(\mathfrak F\) such that for any functor \(F:\mathfrak F\to\mathfrak C\), \(\varinjlim\limits_F\;\mathfrak C\) exists. We say \(\mathfrak F\) is a filtered partially ordered set iff for any \(x,y\in\mathfrak F\), there exists \(z\in\mathfrak F\) with \(z\leq x,z\leq y\). If \(\mathfrak C\subset\textbf{Set}\), the following construction satisfies the colimit diagram.$$\bigsqcup\limits_{x\in\mathfrak F}F(x)/((a,F(\alpha))\sim(b,F(\beta))\text{ iff }\exists\gamma\in\mathfrak F,\;\phi:\alpha\to\gamma,\;\psi:\beta\to\gamma\text{ such that }F(\phi)(a)=F(\psi)(b))$$This relation is only an equivalence relation with the filtered condition on \(\mathfrak F\).
• As an example of the filtered colimit in the previous bullet, letting \(\mathfrak F\) be some filtered poset, and given some functor \(F:\mathfrak F\to Mod_A\), the colimit can be seen as an \(A\)-module as follows: given \(x\in F(A),y\in F(B)\), there exists \(\gamma\) such that \(\phi:\alpha\to\gamma,\;\psi:\beta\to\gamma\) are morphisms in \(\mathfrak F\). Thus, let \(x+y=F(\phi)(x)+F(\psi)(y)\). It's not hard to see that this construction is independent of the choice of \(\gamma\), and gives an \(A\)-module structure to the colimit.
• Given a multiplicative subset \(S\) of a commutative ring \(A\) (i.e., \(S\) is a commutative semigroup), let \(\mathfrak S\) be the category generated by \(S\). Let \(F:\mathfrak S\to Mod_A\) send \(s\to s^{-1}A=\{s^{-1}a\mid a\in A\}\) and send \(\phi:s\to x\cdot s\) to $$F(\phi):s^{-1}a\to (x\cdot s)^{-1}(x\cdot a)$$Under this construction, one can show that \(\varinjlim\limits_F\;Mod_A=S^{-1}A\) via the initial object characterization of the localization. We often write this as \(\varinjlim s^{-1}A=S^{-1}A\). Letting \(S=\mathbb N\), \(A=\mathbb Z\), we have \(\varinjlim\frac1n\mathbb Z=\mathbb Q\).

Adjoints

Let \(F:\mathfrak A\to\mathfrak B\) and \(G:\mathfrak B\to\mathfrak A\) be functors. We say \(F\) and \(G\) are adjoint iff for each \(A\in\mathfrak A\), \(B\in\mathfrak B\), there exists a morphism \(\tau_{A,B}:\Mor_\mathfrak B(F(A),B)\to\Mor_\mathfrak A(A,G(B))\) such that for any \(f:A\to A^*\in\mathfrak A\), the following diagram holds:

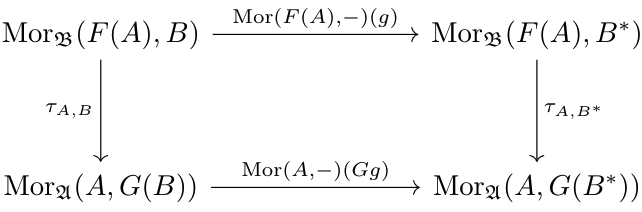
And likewise, for any \(g:B\to B^*\in\mathfrak B\), the following diagram holds:

We call \(F\) the left-adjoint and \(G\) the right-adjoint, and \(F,G\) an adjoint pair.

To see the power of this property, let's replace every \(B^*\) in the diagram above with \(B\), and every \(B\) with \(F(A)\).

Thus, for any function \(g:F(A)\to B\), the above diagram holds. In particular, since \(\id\in\Mor_\mathfrak B(F(A),F(A))\), we have \(\tau_{A,B}(g)=G(g)\circ\eta_A\), where \(\eta_A\) is a function chosen independently of \(B\). In other words, \(\tau_{A,B}\) factors into a component solely dependent on \(A\), and a component solely dependent on \(g\). Likewise for any \(f:A\to G(B)\), we can decompose \(\tau_{A,B}^{-1}(f)\) into a component solely dependent on \(B\), and a component solely dependent on \(f\). We call \(\tau_{A,B}\) natural for this reason.

• Let \(M,N,P\in Mod_A\). Consider the function $$\tau_{M,P}:\Mor_A(M\otimes_AN,P)\to\Mor_A(M,\Mor_A(N,P))$$defined by \(\tau_{M,P}(\psi)(m)(n)=\psi(m\otimes n)\). We call \(\tau_{M,P}\) an uncurry function. It's a trivial application of tensor properties to show that this map is well defined, bijective, and an \(A\)-linear map.

  In fact, defining \(F=(-)\otimes N, G=\Mor(N,-)\) as functors \(Mod_A\to Mod_A\), \(\tau_{M,P}\) happens to be the natural bijection necessary for adjointness of the functors. Given \(A\)-linear morphisms \(f:M_1\to M_2\), \(g:P_1\to P_2\), we have the diagrams

  

  

  It's a cute exercise to see that both of these diagrams hold, which implies that \((-)\otimes N\) and \(\Mor(N,-)\) are adjoint in the category of \(A\)-modules.
• Given any ring morphism \(\phi:B\to A\), there's a canonical contravariant functor \((-)_B:Mod_A\to Mod_B\) which sends the \(A\)-module \(M\) to a \(B\) module \(M_B\) by defining the multiplicative action as \(b\cdot x:=\phi(b)\cdot x\) for \(b\in B\), \(x\in M\). This functor is right adjoint to \((-)\otimes_BA\), since we can define \(\tau_{N,M}:\Mor_A(N\otimes_BA,M)\to\Mor_B(N,M_B)\) as \(\tau_{N,M}(f)(n)=f(n\otimes_B1)\), where \(f(n\otimes_B1)\) is viewed as an element of \(M_B\).

  Given two distinct morphisms \(f,g\in\Mor_A(N\otimes_BA,M)\), there exists some \(n\otimes_Ba\) such that \(f(n\otimes_Ba)\neq g(n\otimes_Ba)\). But, \(f(n\otimes a)=af(n\otimes1)\), and likewise for \(g\). Thus, \(af(n\otimes1)\neq ag(n\otimes1)\), so \(f(n\otimes1)\neq g(n\otimes1)\). This shows that \(\tau_{N,M}\) is injective since \(\tau_{N,M}(f)(n)\neq\tau_{N,M}(g)(n)\).

  Given any morphism \(h\in\Mor_B(N,M_B)\), let \(f\in\Mor_A(N\otimes_BA,M)\) be the map that sends \(n\otimes1\mapsto h(n)\). This definition is well-defined, and has the property that \(\tau_{N,M}(f)=h\). Thus, \(\tau_{N,M}\) is a bijection. In fact, it serves as an adjoint map between the functors \((-)_B\) and \(\Mor_A(N,-)\).

• A classic example of adjoints is groupification. Loosely speaking, it's the process of finding the smallest abelian group containing a semigroup. To formalize this idea, we define the groupification of an abelian semigroup \(S\) to be a map of abelian semigroups \(\phi:S\to G\), with \(G\) an abelian group, such that for any abelian group \(G^\prime\) with abelian semigroup map \(\psi:S\to G^\prime\), the following diagram holds:

  

  This diagram is the dual of the quotient space universal property diagram (not presented on this blog, but it's one of the first ones you'll encounter). This is expected behavior, since quotient spaces are "shrinking" the space, while groupification is "expanding" it. And, since the identity morphism satisfies the universal property for \(\phi\) when \(S\) is an abelian group, the groupification of an abelian group is itself. As such, groupification can be viewed as a closure operator on the category of abelian semigroups. Groupification can also be viewed as a functor from \(\mathfrak S\), the category of non-empty abelian semigroups, to Ab, the category of abelian groups. The inverse of this functor intuitively is the functor that forgets the fact that a given group has inverses and an identity. We call this functor, from \(Ab\to\mathfrak S\), the forgetful functor. Showing that these functors are adjoint (with the forgetful functor as the right adjoint) is a straightforward application of definitions. In general, we expect the forgetful functor to be a right adjoint for any natural functors from a category to a sub-category.

(Mono/Epi)morphisms

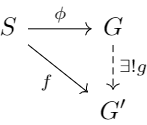
A map \(f:X\to Y\) is a monomorphism if for any \(\phi:Z\to Y\), there is at most one map \(\psi\) satisfying the diagram below.

In other words, if \(f\circ m_1=f\circ m_2\), for \(m_1,m_2:Z\to X\), then \(m_1=m_2\). A map \(f:X\to Y\) is an epimorphism if for any \(\phi:X\to Z\), there is at most one map \(\psi\) satisfying the diagram below.

This is the dual notion to the monomorphism, and can be summarized as \(m_1\circ f=m_2\circ f\) implies \(m_1=m_2\).

• The composition of monomorphisms is monomorphic, and similarly, the composition of epimorphisms is epimorphic.
• By the equivalence of injectivity and left cancelability, and surjectivity and right cancelability for sets, monomorphisms in Set are just injections, and epimorphisms just surjections.
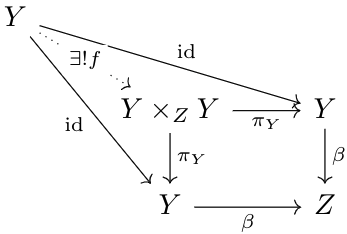
• As we saw before, the commutative diagram representing the universal property for the fibered product \(X\times_ZY\) is below.

  

  Letting \(W=X=Y\), we have

  

  Thus, \(f:Y\to Y\times_ZY\) is defined if \(Y\times_ZY\) is defined. And, \(\beta\circ\id=\beta\circ\pi_Y\circ f\). Thus, \(\id=\pi_Y\circ f\) if \(\beta\) is a monomorphism, which implies that \(f\) is an isomorphism. Thus, the induced map \(f:Y\to Y\times_ZY\) is an isomorphism iff \(\beta\) is a monomorphism.
• Monomorphisms aren't necessarily injective! In fact, they aren't necessarily even functions in any meaningful sense. However, even if monomorphisms are functions, they don't have to behave like an injection. For a rather silly example, consider some non-injective function \(f:A\to B\), consider the category \(\{A,B\}\), with \(\Mor(A,A)=\Mor(B,B)=\{\id\}\), \(\Mor(A,B)=\{f\}\), \(\Mor(B,A)=\varnothing\). Clearly, \(f\) is a monomorphism.

  Similarly, epimorphisms need not be surjections. For example, in the category of rings, the inclusion \(\mathbb Z\to\mathbb Q\) is obviously not a surjection, but since for any \(q\in\mathbb Q\), there exists \(n\in\mathbb N\subset\mathbb Z\) such that \(qn\in\mathbb Z\), there is at most one choice of morphism \(\mathbb Q\to W\) for any \(W\) and morphism \(\mathbb Z\to W\) that satisfies the diagram.

  However, in most settings we care about, this doesn't happen, since the existence of free objects (to be defined in a future post) guarantees that monomorphisms and epimorphisms, if they are functions, are injections and surjections, respectively.