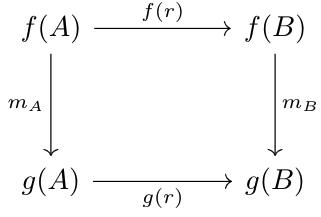Examples of Basic Categories and Tools
Examples of Categories
- The collection of all sets, with \(\Mor(A,B)\) being the set of all functions \(A\to B\), and \(\id_A(x)=x\) for all \(x\in A\) is referred to as Set. Bijections are the isomorphisms of this category.
- The collection of topological spaces, with \(\Mor(A,B)\) the set of continuous maps from \(A\to B\), and the identity map defined as in Set is referred to as Top. Homeomorphisms are the isomorphisms of this category.
- A category in which all maps are isomorphisms is called a groupoid. We can define (although probably shouldn't) a group as a groupoid with a single object.
- For any ring \(A\), we can consider the category of all \(A\)-modules, with \(\Mor(B,C)\) the set of \(A\)-linear maps \(B\to C\). We call this category \(Mod_A\). If \(A=\mathbb Z\), this category is called Ab, the category of Abelian groups, and if \(A\) is a field, this is the category of all vector spaces over \(A\).
- A category with \(|\Mor(A,B)|\leq1\) for all \(A,B\), and with no non-identity isomorphisms is called a partially ordered set. We say \(A\geq B\) iff \(|\Mor(A,B)|=1\). A poset is totally ordered if for any two objects \(A,B\), \(\Mor(A,B)\cup\Mor(B,A)\neq\varnothing\).
- Given a semigroup \((S,\cdot)\), the left category of \(S\) is defined by setting the elements of \(S\) to be the objects, and for all \(x\in S\), add a morphism to \(\Mor(s,x\cdot s)\) for all \(s\in S\). Likewise, we can define a right category. If \(S\) is commutative, we treat it as a category via either of the above constructions.
Important Categorical Tools
A covariant functor from \(\mathfrak A\to\mathfrak B\) is a map \(F:\obj(\mathfrak A)\to\obj(\mathfrak B)\) such that for any \(m\in\Mor(X,Y)\) (\(X,Y\in\mathfrak A\)), \(F(m)\in\Mor(F(X),F(Y))\) is defined. Moreover, \(F(\id_A)=\id_{F(A)}\) for all \(A\in\mathfrak A\), and for any \(h=f\circ g\), \(F(h)=F(f)\circ F(g)\).
A contravariant functor is identical to a covariant functor, but \(F(m)\in\Mor(F(Y),F(X))\), and \(F(h)=F(g)\circ F(f)\).
Vakil's book includes plenty of intuitive examples. From this point on, I'll refer to covariant functors when I say "functor", unless otherwise specified.
In some sense, functors are the "morphisms" of categories. So it's reasonable to ask, are there functors of functors? Let \(f,g:\mathfrak A\to\mathfrak B\) be covariant functors. \(H:f\to g\) is a natural transformation if it maps each \(A\in\mathfrak A\) to a morphism \(m_A:f(A)\to g(A)\), and for each \(r\in\Mor(A,B)\in\mathfrak A\), the diagram below holds.
Natural transformations can also be defined for contravariant functors, with some of the arrows flipped.
Similar to morphisms, we say that two categories \(\mathfrak A,\mathfrak B\) are isomorphic (although to distinguish this from other isomorphisms, we call these equivalent) if there exists a functor \(F:\mathfrak A\to\mathfrak B\) which is an isomorphism. More simply put, there exists \(G:\mathfrak B\to\mathfrak A\) with \(F\circ G\) and \(G\circ F\) isomorphic to the identity functors \(\id_{\mathfrak A},\id_{\mathfrak B}\).
A beautiful result is that a functor \(F:\mathfrak A\to\mathfrak B\) is an isomorphism if it is fully faithful, i.e., for all \(A,B\in\mathfrak A\), \(F:\Mor(A,B) o\Mor(F(A),F(B))\) is a bijection, and if it is essentially surjective, i.e., for all \(C\in\mathfrak B\), there exists \(A\in\mathfrak A\) and an isomorphism \(g\in\Mor(F(A),C)\).
For an example of a contravariant functor, let \(A\in\mathfrak A\) be an object of a category. Thus, there is a contravariant functor \(h_A:\mathfrak A\to\textbf{Set}\) given by \(h_A(B)=\Mor(B,A)\), and for any \(f\in\Mor(B,C)\), \(h_A(f):\Mor(C,A)\to\Mor(B,A)\) is defined as \(h_A(f)(g)=g\circ f\). This functor is called the functor of points. We often write the functor of points as \(\Mor(-,A)\) to represent the fact that we map an object \(B\to\Mor(B,A)\). Likewise, we can talk about the covariant functor \(\Mor(A,-)\) which sends \(B\) to \(\Mor(A,B)\).