Why bother with Categories?
The definition of a category seems somewhat uninspired when you first encounter it. What are "objects"? What are "morphisms"? Why bother creating a notion of a category?
Russell's Paradox
The most obvious reason is Russell's paradox. We want a way of dealing with large collections of objects without running into set-theoretic issues. So unlike sets, which allow for comprehensions over all of its members simultaneously via the axiom of specification, categories only allow you to access data on its members locally, via observing the maps between any pair of objects.
But this reason alone isn't sufficient to bother working with categories. In fact, if our sole goal was to create a powerful extension of ZFC to arbitrary classes, we would end up with NBG set theory.
Universal Properties
The second reason we care about categories is that it allows us to formulate universal properties in a very convenient fashion. Vakil presents the following example:
Generally, we define the cartesian product of sets as follows: $$M\times N=\{(m,n)\mid m\in M,\;n\in N\}$$But what if we defined the cartesian product as $$M\times N=\left\{{m\atop n}\mid m\in M,\;n\in M\right\}$$Most likely, you'd have no issue with this, as you'd easily identify the contents of these definitions to be identical. But from a symbolic standpoint, it's not obvious at all that these two representations have the same information content. Instead, if we came up with a definition based on the information content of \(M\times N\), we'd be able to identify these definitions as identical.
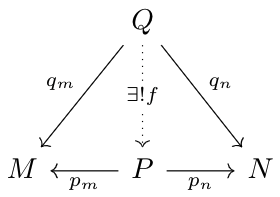
Instead, category theorists define the cartesian product of \(M,N\) as the \(P\) that satisfies the commutative diagram.
The idea is that the cartesian product is some set \(P\), with projection maps \(p_m,\;p_n\) to \(M,N\), such that for any \(Q\) that also projects onto \(M,N\) via maps \(q_m,q_n\), there exists a unique \(f\) such that \(q_m=p_m\circ f\), \(q_n=p_n\circ f\). In other words, any set that projects onto \(M,N\) factors those projections through \(P\).
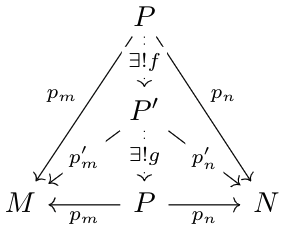
The beauty of this definition is that it implies that if \(P\) exists, it is unique up to isomorphism. To see why, assume that \(P,P'\) with maps \(p_m,p_n,p'_m,p'_n\) satisfies the graph. Then, consider the following diagram:
Both \(f\) and \(g\) are unique and thus, their composition must be unique. But, \(\id_P\) is a map that satisfies \(p_m\circ\id_P=p_m\) and \(p_n\circ\id_P=p_n\), so \(g\circ f=\id_P\). A symmetric argument shows that \(f\circ g=\id_{P'}\), which shows that \(P,P'\) are isomorphic, as \(f,g\) are inverses.
This tells us that this definition is more than just a duck test, as it guarantees that if we can find an object \(P\) that satisfies the diagram, we can call that object the product, since any other object satisfying the diagram will be isomorphic to \(P\). This is a common theme for universal properties: the diagram itself will imply the uniqueness of any solution to the diagram. The simplicity of expressing these relations in category theory is what lends the field so much power.