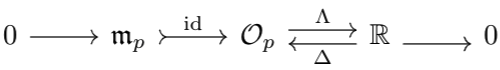Understanding Sheaves
Unlike with categories, where I provided a definition first, and then provided some intuition as to why you should care, I'll first show you why you might care, and then define what a sheaf is in a later post.
Motivation and History of Sheaves
The power of category theory comes from the observation that it is the morphisms, not the structure itself, that holds the meaning of the spaces we care about. The kernel object by itself, for example, is completely meaningless without an embedding map. The product object is similarly useless without projection maps.
Still, it may be surprising how effective understanding geometric spaces via nice morphisms on the space is. Differentiable manifolds can be entirely classified via chart maps onto Euclidean space. This example is especially important, since for most manifolds of interest, there aren't maps from the entire space onto Euclidean space, but rather just open subsets of the manifolds. This idea will be generalized in sheaves.
Sheaves were first introduced by Leray in the 1940s, and Serre was the first to introduce the notion to algebraic geometry. The term sheaf arises from the agricultural lexicon, referring to a collection of stalks (why this is relevant should make itself obvious over the series of posts on this part).
Motivating Example
On any \(\cC^1\) manifold \(X^n\) (\(X^n\) just means \(X\) has dimension \(n\)), (if you aren't comfortable with manifolds, just consider \(X=\bbR^n\)), and any open set \(U\subset X\), there exists a ring of differentiable functions \(U\to\bbR\), which we'll call \(\cO(U)\).
What are nice properties of this ring we might want to codify in sheaves?
- For any open subset \(V\subset U\), all of the differentiable functions on \(U\) should restrict onto differentiable functions on \(V\). In other words, there should be a restriction map \(R_{U,V}:\cO(U)\to\cO(V)\).
- Now suppose we have the following chain of open subsets of \(X\): \(W\subset V\subset U\). Thus, it shouldn't matter whether we restrict a function on \(U\) directly to \(W\), or restrict it via first restricting to \(V\) and then to \(W\). So, we expect \(R{V,W}\circ R_{U,V}=R_{U,W}\).
- If we have an open cover \(U_i\) of \(X\), and two functions \(f,g\) that agree on each \(U_i\), then \(f\) should equal \(g\) globally. More precisely, if \(R_{X,U_i}(f)=R_{X,U_i}(g)\) for all \(i\), then \(f=g\). This seems obvious but it gives us a way to prove something global from local observations.
- As a corollary to this, suppose you have the same open cover of \(X\), and for each \(i\), you have a differentiable function \(f_i:U_i\to\mathbb R\) such that for any \(i,j\), \(R_{U_i,U_i\cap U_j}(f_i)=R_{U_j,U_i\cap U_j}(f_j)\) (i.e., on the intersection of the domains, the functions agree). Then, we should be able to string together the locally defined functions into a global function by defining \(f:X\to\mathbb R^n\) as the function which evaluate an element of \(U_i\) the same way \(f_i\) does. More formally, there should be some \(f\in\cO(X)\) such that \(R_{X,U_i}(f)=f_i\) for all \(i\). Ensuring that this definition is well-defined is easy on differentiable manifolds, but your intuition should tell you that this process isn't trivial on weirder spaces.
From now on, given any function \(f\in\cO(U)\), we'll define \(f\vert_W\) for \(W\subset U\) as \(R_{U,W}(f)\).
Note that this relation is only an equivalence relation iff the set of open sets containing \(p\) is filtered under the partial order of inclusion; i.e., for any open sets \(U,V\) such that \(p\in U\cap V\), there exists some open \(W\) such that \(p\in W\subset U\cap V\). We call a collection of open sets satisfying the filtered condition a neighborhood basis or just a base of \(p\).
Intuitively, the stalk represents the set of "shreds", which we call germs, of differentiable functions around point \(p\).
The appearance of the filtered condition and the definition of the germ should remind you of the Set characterization of the filtered colimit in Universal Properties. In fact, via the following construction, we can define the stalk as a colimit.
Given a base \(\rmB\) around \(p\) (which as observed in the previous definition is a filtered partially ordered set category), we can define a function \(\cO_p^*:\rmB\to\textbf{Ring}\) which sends \(U\mapsto\cO(U)\) and \(U\to V\) to \(R_{U,V}\) (since \(U\to V\) means \(V\subset U\)). Thus, the stalk of \(p\) is \(\mathcal O_p=\varinjlim\mathcal O_p^*\). With these two alternate characterizations of the stalk, we now know the following things about the stalk purely by definition.
- It always exists, given a neighborhood base around the point.
- It is a ring, since it is an element of Ring.
- There exists a natural embedding \(\cO(U)\to\cO_p\) for all \(U\).
Let \(\mathfrak m_p\) be the set of functions \(f\) in \(\cO_p\) such that \(f(p)=0\). Observe that if \(f,g\in\mathfrak m_p\), \((f+g)(p)=f(p)+g(p)=0\). And, if \(h\in\cO_p\), $$f\cdot h(p)=f(p)\cdot h(p)=0$$Thus, \(\mathfrak m_p\) is an ideal. I claim that \(\mathfrak m_p\) is maximal.
To see why, for any \(r\in\mathbb R^n\), let \(\Delta r\in\cO_p\) be the constant function sending everything to \(r\). Let \(\Lambda:\cO_p\to\bbR^n\) be the evaluation map at \(p\). Thus, \(\Lambda\circ\Delta=\id_\bbR\). And, by definition, \(\mathfrak m_p\) is the kernel of \(\Lambda\). Thus, the following is a split short exact sequence:
Not only does this imply that \(\cO_p/\mathfrak m_p\cong\bbR\), but that \(\cO_p\cong\mathfrak m_p\oplus\bbR\) by the splitting theorem shown in (Co)homology and Exactness. Since \(\bbR\) is a field, \(\mathfrak m_p\) is maximal.
And, there are no other maximal ideals since for any function \(f\in\mathcal O_p\) with \(f(p)\neq0\), there exists an open set \(V\) around \(p\) such that \(f\) is non-zero on \(V\) (WLOG we can choose \(V\) to be relatively compact), and thus an open set \(W\) in the base with the same property. Thus, in \(W\), define \(f^{-1}(x)=f(x)^{-1}\). Note that \(D f^{-1}(x)=\frac{D f(x)}{f(x)^2}\) which is well defined on \(W\), so thus \(f^{-1}\) is differentiable on \(W\). So \(f\) is a unit as desired.